.
Hier volgt een impressie van een periode meetkunde in de 6e klas.
eerste week
Wie ‘meetkunde’ zegt, bedoelt meestal o.a. het tekenen van cirkels, driehoeken en andere meetkundige figuren; het leren van de eigenschappen daarvan om met deze eigenschappen te kunnen bewijzen.
Tekenen van vormen die in de meetkunde terug te vinden zijn, doen de kinderen al zo gauw ze in de 1e klas zitten, wanneer ze op hun eerste schooldag al bewuster kennis maken met de ‘rechte’ en de ‘ronde’.
Die worden dan in allerlei vormcombinaties geoefend en worden ook toegepast bij het schrijven in hoofdletters*.
Maar ook de kleuter gebruikt, soms letterlijk met verve, de rechte en de ronde wanneer hij z’n ‘oer’zon tekent: de cirkel en de stralen(!).
In de pedagogische voordrachten is er ook sprake van meetkunde tussen het 9e en het 11e, 12e jaar. Zie: Meetkunde(1)
Maar in de 6e klas gaat het nog om meer. Vanaf de geboorte al, natuurlijk, maakt het denken een ontwikkeling door. Voor de kleuter en de 1e-klasser bijv. is dit nog een (zeer) beeldend denken. De ‘onmogelijkheden’ in de sprookjes zijn met zijn manier van denken mogelijk. Dat verandert bij het ouder worden: de sprookjes worden ‘kinderachtig’, terwijl er een groot verlangen blijft de soms eveneens ‘fantastisch’ klinkende verhalen uit de mythologieën te horen.
Hand in hand met de ontwikkeling van het denken gaat o.a. ook het krijgen, hebben of houden van een eigen mening. De kinderen ‘vinden’ ergens iets van. Waarom? ‘Nou, gewoon, daarom!’ Echt verwoorden is nog heel moeilijk. Ze vinden het ‘leuk’ of ‘stom’.
Je zou dit gerust een ‘subjectief standpunt’ mogen noemen.
En subjectieve standpunten houdt de mens zijn hele leven! Vandaar de vele meningsverschillen.
Maar er komt ook een ogenblik in het leven dat er naast dit subjectieve voelen en denken nog een ander vermogen ontstaat: je te verplaatsen in het standpunt van de ander, of het andere. Je eigen mening los te laten; tot andere inzichten te komen. Denken, dat losser komt te staan van je eigen beleving; dat in dat opzicht minder beleefbaar, minder concreet wordt, dus abstracter.
En dat vermogen krijgt de mens met de puberteit. Maar dan worden ook de gevoelens veel heftiger: ‘storm en drang’!
En dus is het goed om aan de vooravond van nog meer subjectiviteit ook de ontwikkeling van het van nature gegeven vermogen om te objectiveren ter hand te nemen.
Vanaf dit 11e,12e jaar laat Steiner al die vakken beginnen waarin deze objectiviteit gevraagd wordt; waar oorzaak en gevolg heersen, dat de kinderen door hun groeiende vermogen tot inzicht, nu ook gaan ‘snappen’.
Wij allemaal hebben over van alles en nog wat een mening; we doen dingen op een bepaalde manier. Waarom? Vaak weten we dat niet eens (meer).
Wie (’s avonds?) zichzelf nog eens in een soort ‘terugblik’ bekijkt en op de plaats van een kind in zijn klas gaat zitten en vandaar naar de meester of juf die jij bent, kijkt, zal veel aan zichzelf leren opmerken. Veel heen en weer lopen voor de klas (waarom eigenlijk); half op je bureau gaan zitten (daar is een bureau niet voor) (waarom eigenlijk) zal zich veel meer bewust worden van hoe hij of zij voor de klas staat (of zit) – in veel meer dan letterlijke zin -.
Om tot de conclusie te kunnen komen dat je niet eens echt weet waarom je dingen wel of niet doet. Of dat je bij nader zoeken tot de conclusie komt, zoals ik, dat ik een aantal dingen deed, omdat ik die ooit van mijn meester zag, toen ik als kind bij hem in de klas zat!
Daarmee neem je een bepaalde plaats in. Je hebt een standpunt. Je staat ergens (voor). En meestal blijft het daarbij. De verharding van standpunten duidt daarop. Er wordt zelfs gesproken over ‘ingraven’.
Hoe vaak gebeurt het niet dat een ander ons voorhoudt hoe we, wat we deden, ‘beter zo kunnen doen’. Waarom? Omdat die ander dat vindt! De manier waarop jij het doet is minstens net zo goed, maar anders. En om zover te komen dat je dat andere als net zo waardevol kunt zien als jouw opvatting, kost heel veel moeite; meestal komt het er niet van – in dat ver-plaatsen – in de ander: dus een ander standpunt in te nemen.
Rudolf Steiner:
‘Wanneer een boom van verschillende kanten wordt gefotografeerd, is het nog steeds dezelfde boom, maar de foto’s zien er heel verschillend uit; zo kan ook ieder mens zijn eigen mening hebben – afhankelijk van het standpunt waarop hij zich plaatst.’ [1]
Toen ik een meetkundeperiode in de 6e klas moest geven, vond ik in bovenstaand citaat een inspiratie tot een bepaalde manier om de eerste les mee te beginnen.
De eerste dag van de periode
Ik vroeg twee kinderen, los van elkaar, naar buiten te gaan, de een naar de voorkant van de school, de ander naar de achterkant en gaf ze de opdracht mee zoveel mogelijk details te kunnen geven. Als ze weer terug waren in de klas, mochten ze wél de details noemen, maar niet het woord ‘voor- of achterkant’ ‘van de school’ enz. gebruiken, niets wat direct naar het schoolgebwouw verwees. Eenmaal terug in de klas vertelde de een, toen de ander, wat ze hadden waargenomen. Prachtig stonden twee verschillende beschrijvingen – eigenlijk twee standpunten – tegenover elkaar. Het duurde enige tijd voordat een leerling en even later ook andere een vermoeden kregen dat hier sprake was van het schoolgebouw. Uiteindelijk konden we de verschillen goed aanduiden, maar moesten ook tot de conclusie komen, dat het over een en hetzelfde gebouw ging! En dat dus de ene opvatting niet meer of minder waar(d) was, dan de andere.
Daarover kun je dan met een klas heel goed spreken en als dit onderwerp eenmaal bewuster door de leerlingen wordt doorzien, kunnen ze ook ‘zomaar’ eigen door- of meegemaakte ervaringen weergeven.
Met dit gegeven gingen we naar de gymzaal en daar vroeg ik de kinderen in een kring te gaan staan, maar wel een die precies rond was. Daar stonden de kinderen dan ‘op hun standpunt’; maar aangezien de kring geen cirkel vormde, moesten er nog wat verplaatsingen plaatsvinden. ‘Jij moet naar voren’; ‘nee, jij moet naar achter’; ‘ja, maar dan staat hij niet goed!’ Enz.
“Maar hoe weet je dat,’ bracht ik er tegenin, ‘wie bepaalt dat?’ ‘Wie zou ons kunnen helpen?……Of wat?’ ‘Meten!’, riep een kind. ‘Ja, met een touw!’, een ander.
En inderdaad: het touw als objectief ding, bracht de oplossing. Iemand hield het vast op het middelpunt, een ander aan het uiteinde en waar dit verscheen moesten de leerlingen hun standpunt innemen: een prachtige cirkel – precies rond dus – was ontstaan. Zonder meningsverschil van ‘jij moet vooruit, nee jij achteruit!
En in het touw zagen de kinderen gemakkelijk de passer die voor de objectieve rondheid van de cirkel garant staat.
Terug in de klas begonnen we cirkels te tekenen. Nog niet met de passer, maar ‘uit de hand’. En zo rond mogelijk, natuurlijk.
Dat valt nog niet mee:
 .
.
Heel vaak komen de kinderen met herinneringen aan ‘vroeger’, toen ze in de kleuterklas of later ‘een zon’ of iets anders rond, tekenden.
De passer moet er natuurlijk aan te pas komen.
Goed gereedschap is ook hier het halve werk. Mijn ervaring is dat je het beste zelf de passers kunt aanschaffen en deze door de kinderen laat gebruiken. Sommige scholen laten de ouders voor de passers betalen. Alles heeft z’n voor en tegen; als de passer kwalitatief maar goed is.
Uiteraard heb je passerpotloodstift bij de hand en ieder kind moet een klein stukje schuurpapier hebben (korrel 80 of 100) om steeds voor een scherpe punt te kunnen zorgen. Het afgeschuurde vlakje bevindt zich aan de buitenkant van het passerbeen.
In zijn boek ‘Geometrie durch übende Anschauung’ [4] zegt de auteur Alexander Strakosch over het gebruik van de passer:
‘Bij het tekenen van een cirkel, neem je de passer bij de kop, het deel boven het punt waar de benen samenkomen. De kop houd je zo loodrecht mogelijk, tussen duim en wijsvinger van de (rechter)hand. Dan zet je de punt op het papier en draai je eerst een rondje boven het papier – tegen de wijzer van de klok in. Dan op het papier en draai je in één beweging de hele cirkel. De potloodpunt moet deze vorm hebben (zie boven). Het schuinmaken gebeurt met schuurpapier. De niet-geschuurde kant wijst naar binnen. Daardoor wordt bereikt dat bij het stomper worden van de punt de aan de binnenkant getekende lijn toch nog op dezelfde afstand blijft. Tijdens het tekenen moet de passer zo loodrecht mogelijk blijven. Moet de punt op een bepaalde plaats komen te staan, gebeurt dit met de linkerhand en de rechter houdt de passer vast.’
(Ik heb zelf een passer die je moet vasthouden aan een klein staafje dat je eraf kunt schroeven. Als ik de cirkel naar links teken, gaat dat staafje los (omdat je het naar rechts vastdraait). Tegen de wijzers van de klok gaat dan dus niet.)
Als je de eerste dag niet meer aan de passer toekomt, kan het teleurstellend zijn voor de kinderen, wanneer ze zelf de passer – op de 1e dag van de meetkundeperiode – bij zich hebben; waneer je hem uitdeelt, heb je altijd de mogelijkheid om met de belofte ‘morgen de passer’, iets in de kinderen op te roepen van ‘ha, morgen…’
Als dan de passer op tafel ligt, nadat er van alles over is verteld (benen, waar vast te houden, hoe te draaien, hoe lang de punt, waar afgeschuurd, enz), komen er echte cirkels.
Het kleuren gebeurt meer om alles ‘mooi’ af te werken. (Hier bijna letterlijk: af te ronden).
Ze kunnen eerst los van elkaar staan, later elkaar overlappen.
Hier is steeds sprake van ‘willekeurig’.
.
 .
.
Je kunt natuurlijk je eigen methode ontwerpen – je eigen weg om er te komen.
Ik geef hier een bepaalde werkwijze aan, die zeker niet DE werkwijze is, maar ‘een’, dat is zo mooi aan het vrijeschoolonderwijs: dat je, je baserend op de uitgangspunten – de menskundige – langs je eigen weg kunt streven om het gegeven doel te bereiken.
Een tweede dag
Je zou nu verder kunnen gaan met de cirkel, maar je zou ook naar de tegenstelling, de rechte lijn kunnen gaan. Zodat je a.h.w. – 6 jaar later – nog eens met de rechte en de ronde bezig bent (wat kinderen zich meestal goed herinneren. Het gevoel kan ontstaan dat we in de 1e klas iets deden, wat nu in de 6e terugkomt – anders, want wij zijn anders geworden. Maar ook: de lesstof hangt op deze school met elkaar samen.)
Het is goed om iedere dag, vóór je weer verder gaat, te herhalen, wat er de vorige dag is gedaan. Je kunt de leerlingen dat bewust maken: een soort ‘huiswerk’ met de opdracht: morgen kunnen vertellen wat we gedaan en/of geleerd hebben. Je kunt ze dat zelfs in een schrift(je) laten opschrijven.
(Hier staat over de manier van herhalen een uitleg)
Wat je, aan welk kind, vraagt, kun je nog nader laten afhangen van hoe het kind is.
In GA 302 behandelt Rudolf Steiner verschillende typen kinderen. Hij geeft daarbij ook aan, hoe je deze, door het op een bepaalde manier gebruiken van leerstof, kunt helpen bij hun ontwikkeling.
(Het voert hier nu te ver om er dieper op in te gaan en op deze blog is daar nog geen aandacht aan besteed. In ‘De menseljke ziel – en de twee stromen uit het tweede hoofdstuk van de ‘Allgemeine Menschenkunde’ heeft Kim Lapré dat gedaan. [2])
Willekeurige lijnen:

Vanaf een middelpunt:

Ook naar een middelpunt toe.
Dan is het zaak de ogen op dat middelpunt te laten rusten en naar dat punt te blijven kijken, terwijl je de lijn trekt. Vergelijkbaar met het boogschieten: naar de roos kijken; of op de evenwichtsbalk: niet naar de balk kijken, maar naar je eindpunt.

Vanuit een middelpunt: even lange lijnen en naar een middelpunt toe: Dat valt uit de hand niet mee: we hebben de passer nodig.

Deze tekening werd door de kinderen herkend als ‘wat we in de gymzaal deden’.
Naast de passer is ook de liniaal een onmisbaar gereedschap.
Hij maakt een rechte lijn, zoals de evenaar, de linie. (Zo onthoudt je ook dat het is linIaal en niet linEaal – dat heeft de afleiding lineair!)
Ook deze moet nog even opnieuw (die is tenslotte al behandeld in de 4e klas) in de aandacht komen, waar het gaat om: waar is het begin: meestal niet aan het fysieke begin, maar even verderop, bij de 0.
En niet alles hoeft met kleur:

Als de opdracht was: vanuit het middelpunt naar de rand, dan zijn sommige lijnen niet precies genoeg; bij de omgekeerde opdracht, trouwens, ook niet. Dat moet dus nog mooier = preciezer!
Het begrip ‘onwillekeurig’ – geen eigen willekeur – kan hier zijn intrede doen. Je bent niet vrij meer om ‘zomaar’ lijnen te trekken: vanaf of naar het middelpunt toe, ligt vast. Wáár je ze tekent: dat is nog willekeurig.
Zo kun je willekeurige lijnen van rand naar rand tekenen:

‘Rand’ ja, het is de rand, maar in de meetkunde waar zoveel lijnen gebruikt worden, krijgen vele lijnen een eigennaam, zoals jullie om te onderscheiden wie wie is, of hier: wat wat is. Hoe zou je deze ‘rand’ kunnen noemen?’
Het is interessant om te zien welke antwoorden er kunnen komen. Soms zijn ze mooier dan de officiële naam. ‘Cirkellrand’, ‘cirkelgrens’, cirkelomlijsting’. Dan is de officiële naam soms wat ontnuchterend.
‘Neem een opening tussen de benen van je passer (ook zo’n uitdrukking vraagt soms enige aandacht…) en kijk – in gedachten – hoe groot die cirkel wordt. Dan teken je hem met de passer. Wat doe je eigenlijk?’ Dan valt het woord ‘omtrekken’, ‘omtrek’ en daar houden we het op. De omtrek van de cirkel. En omdat het ook een lijn is, dus ook: omtrekslijn.
We kunnen achter in het periodescchrift bijv. een woordenlijst aanleggen met de woorden die we leren.**
De lijnen mogen elkaar – weer een nieuw begrip – ook snijden:

Wat is de grootst mogelijke lijn in een cirkel?
“We doen wel ‘meetkunde’, maar we gaan de lijnen binnen de cirkel niet met de liniaal meten. Hoe weten we dan, welke de grootste is.’

Nu moet er ontdekt worden dat de grootste lijn binnen de cirkel over het middelpunt loopt. Hoe zou zo’n lijn genoemd worden? Dat ligt voor de hand: midden-; middellijn. En het punt waar deze doorheen gaat? Middenpunt; middelpunt.
Vanuit een soort ‘natuurgevoel’ trekken de meeste kinderen de middellijn horizontaal. En op de vraag hoe het nog meer zou kunnen, volgt de verticale. Dat ook diagonale lijnen kunnen, dat is verrassend. ‘Teken maar eens wat middellijnen. Wel exact door het middelpunt, hè!’
Dus: goede puntenslijper voor scherpe punten!

Nu zou een (huis)werkopdracht kunnen zijn: hoeveel middellijnen zitten er dan wel niet in een cirkel? Kijk naar je eigen tekening en denk, zie voor je, waar er nog meer passen.
En dan ontdekken de kinderen dat er heeeeeeel veel in kunnen; je kunt ze niet tellen, eigenlijk. Dus ‘DE’ middellijn betaat niet. Er is ‘EEN’ (één of un, dat valt hier samen) middellijn. Hiermee is het begrip ‘middellijn’ beweeglijk geworden, zoals hier het begrip driehoek. Een middellijn, of de(ze) middellijn in deze cirkel, is de geconcretiseerde, ‘stilgezette’ middellijn uit al die ‘bewegende’ (a.h.w. ronddraaiende) middellijnen.
Hier hebben we dus kunnen ‘karakteriseren’ i.p.v. ‘definiëren’.
De definitie komt er aan! Maar eerst het levende beeld: Rudolf Steiner – wegwijzer 15
Uiteraard kun je nog meer tekenvariates bedenken; je kunt ze eerst oefenen op oefenpapier en de kinderen dan de mogelijkheid geven de in hun ogen best geslaagde tekeningen in hun periodeschrift te tekenen.
Een derde dag
Wat betreft de verdeling van de stof over de verschillende dagen, zij opgemerkt dat dit slechts zeer willekeurig is. De ene klas werkt harder dan de andere; valt je periode in de advent- en kersttijd is wellicht het hoofdonderwijs korter door andere activiteiten, enz.
Wanneer het gaat om ‘zich iets voor te stellen’ kun je dit op verschillende manieren benaderen. In de tweede voordracht van de ‘Algemene menskunde’ [3] doet Steiner dit bijv. vanuit het standpunt ‘verleden en toekomst’. Het voorstellingsbeeld van het verleden is het bekende herinneringsbeeld (“Denkend aan Holland, zie ik….”) en het beeld van wat er concreet nog niet is: het fantasiebeeld, de imaginatie. Je voorstellen hoe iets gaat worden, eruit zal gaan zien, is toekomst en derhalve verbonden met de wil. Steiner heeft hierover veel gezegd, al karakteriserend vanuit verschillende standpunten. ‘De wil in het denken brengen’ betekent het denken verlevendigen, vitaliseren. Dat is bijv. wat er bij mediteren kan gebeuren.
Met het oog op dit ‘vooruit denken’ gaf ik de kinderen deze opdracht:
‘Stel je voor, je hebt een schoteltje of een euro, in ieder geval iets wat rond is. Daar precies onder is nog zo’n schoteltje of euro, of wat je hebt. Deze onderste komt langzaam te voorschijn (of de bovenste schuift langzaam weg). Wat zie je dan. Teken dit uit de hand. Het schuift steeds verder: teken verschillende stadia van dit wegschuiven.
Ook dat is niet makkelijk.
Al die jaren dat we vormtekenden, mochten de kinderen in hun tekening die ze gemaakt hadden, verbeteringen in de vorm aanbrengen, a.h.w. vanuit hun eerste poging corrigerend werken. Dat kun je hieronder nog zien:.
.
Interessant voor ‘de bewegende voorstelling’ is, dat er door de kinderen allerlei verschillende vormen worden gemaakt:
staand, maar ook liggend (er was bij de opdracht geen richting aangegeven):
Door ze met elkaar te vergelijken, zie je dat er ‘oneindig’ veel mogelijkheden zijn. Het is a.h.w. net als met de hoeveelheid middellijnen in een cirkel.
(Wanneer kinderen eens sneller klaar zijn met een opdracht, kun je ze altijd stimuleren bovenstaande tekeningen met de hand nóg preciezer uit te voeren).
Als dan duidelijk is geworden dat de schuivende cirkels in allerlei stadia getekend kunnen worden, is het weer tijd voor de passer.
.
Als je de eis gaat stellen dat de cirkels niet naar links of rechts mogen afwijken, klinkt al snel ‘in een rechte lijn’.
Waar komt die lijn dan?
Dat is niet zo moeilijk:

Uiteraard kan deze ook verticaal staan. Maar hoe nog meer?
Ook: diagonaal
Wanneer de kinderen de opdracht met de diagonaal krijgen, komen er natuurlijk weer net zoveel verschillende tekeningen als er leerlingen zijn. En als we de tekening opzoeken met alle middellijnen, wordt het duidelijk dat op al die middellijnen al die cirkels kunnen. Dat ‘beweeglijk’ denken is een mooie opgave; probeer het zelf eens: de middellijn die als een kompasnaald zich beweegt van noord over oost, zuid en west weer naar noord (of omgekeerd) en op de kompasnaald van boven naar beneden (of omgekeerd) al die zich verschuivende cirkels. Wat een beweging!!
Maar, we gaan de beweging ook weer bevriezen. En heel eenvoudig maken. We nemen maar 2 cirkels die van elkaar verschuiven, zoals we waren begonnen. Nu moeten ze echter in een positie komen die ‘evenwichtig’ is – we kunnen herinneringen ophalen aan de 2e klas toen we voor het eerst symmetrietekeningen oefenden:

[3]
Kleur wat ze geneenschappelijk hebben. Het is belangrijk dat de kinderen leren zien dat er ‘iets’ is wat behoort bij zowel de ene als de andere cirkel:
Een vierde dag
Uiteraard kun je ook 3 schoteltjes of euro’s op elkaar leggen en deze laten verschuiven. De 3e kan t.o.v. de andere 2 weer allerlei verschillende plaatsen innemen. De voorstellingsoefening kan worden uitgebreid. Laat de kinderen zelf eens beschrijven hoe zij de beweging van al deze cirkels voor zich zien.
Je kunt nu de werkwijze van ‘met twee cirkels’ ook gaan uitvoeren met 3:
eerst uit de hand:
Meerdere cirkels erbij:
En dan weer met de passer. We hebben al geleerd dat het, om het precies te doen, nodig is, lijnen te trekken. En omdat we in de meetkunde alles precies willen doen, gaan we nu, kijkend naar de tekening die je gemaakt hebt uit de hand – die hierboven staat dus – de lijnen denkbeeldig trekken: vóór ons zien.
Die lopen zo:
Nu gaan we deze tekening niet nog eens maken en dan met de passer; we gaan meteen naar een symmetrie: hoe ziet die eruit?
Kun je je dat weer voorstellen. Waar stopt – in die hele kluwen van bewegende cirkels – die ene vorm. Als je denkt hem te hebben, kun je hem even schetsen en daarna uitvoeren met de passer: 
Er staat in deze tekening iets wat je niet echt nodig hebt. Zie je dat?
Dat blijken de lijnen te zijn. Hoe kun je dan toch de symmetrie krijgen?
Door het passerpuntje (in het papier) van de ene cirkel te gebruiken voor de andere. Hier ontdekken de kinderen iets wat later aan de orde komt, nl. de cirkels hebben gemeenschappelijke middelpunten (door de even grote straal))
Tekenen en de gemeenschappelijke vlakken kleuren. Dat roept natuurlijk ook het kleuren van de andere vlakken op.
Ieder kind neemt natuurlijk zijn eigen kleuren, zodat er binnen het vaste gegeven een grote verscheidenheid aan uitvoering uitstaat.
Nu dit eenmaal is gedaan en door de kinderen voor zover ze daartoe in staat zijn, dit hebben kunnen ‘denken’, gaan we verder met 4 cirkels.
Meestal verliet ik hier de procedure die ik vanaf het werken met de 2 cirkels had gevolgd. Je nog méér ‘beweeglijk’ voorstellen, gaat met 4 cirkels bijna niet meer en als het je als leerkracht is gelukt om het de leerlingen met de middellijnen en 2 of 3 verschuivende cirkels te laten uitvoeren, heb je m.i. de kinderen voor het eerst kennis laten maken met ‘beweeglijke begrippen’.
Er ontstaat een ‘centrale’ cirkel, waarop de andere worden getekend.
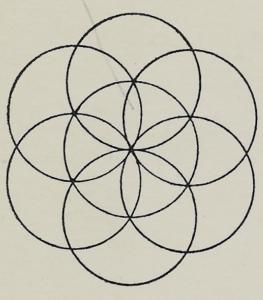
Zo bouw je verder met de 5e en de laatste, de 6e . De figuur heeft dan 7 cirkels.
Een optimale symmetrie is bereikt:
Die nu naar eigen fantasie (en schoonheidszin) te mogen kleuren, is voor de meeste kinderen een feest.
Er waren altijd wel kinderen die ze (samen) op het bord wilden maken – met de bordpasser – of deze wilden gebruiken om op de grond op grote vellen papier een grote vorm te maken om die met bordkrijt te kleuren. Zelfs op het schoolplein met stoepkrijt.
Hier staan er verschillende afgebeeld onder nummer 1
Een vijfde dag
Het zou mooi zijn wanneer je bovenstaande lesstof in 1 week zou kunnen behandelen. Wanneer dat niet lukt: geen nood. Je kunt het beter langzamer doen en goed, dan dat je te snel gaat en geen tijd hebt om alles goed te laten aankomen.
Zo’n laatste dag leent zich ook om alles mooi af te werken, af te maken. De ‘bloemen’, zoals de kinderen vaak de tekening met de 7 cirkels noemen, vragen echte aandacht en zorgvuldigheid.
Toen we in de lagere klassen de vormtekeningen ‘in’kleurden, had dat eigenlijk met vormtekenen niet eens zoveel te maken. Voor het maken van de vorm als ‘spoor van een beweging’ had je het inkleuren of ‘versieren’ ook weg kunnen laten.
Bij de zojuist ontstane cirkelvormen is dat niet het geval. De strenge wetmatigheden komen pas echt tot hun recht als ze zichtbaar worden door de kleur. Door hun grotere gecompliceerdheid dan de vormtekeningen, kan het geven van verschillende kleuren ook zichtbaarder maken, waar je naar op zoek bent, of wat je wilt vinden.
Maar door hun strenge symmetrie zichtbaar te maken d.m.v. kleur breng je ook een nieuw element in: dat van het kunstzinnige. De alom geprezen schoonheid van de vormen, wordt nog eens versterkt door -genuanceerd – aangebrachte kleur.
Dat zou je op de 5e dag, of later, of telkens aan het eind van het hoofdonderwijs kunnen doen:
met wat tot nu toe geleerd is, nieuwe vormen scheppen en kunstzinnig afronden.
De kinderen zullen gemakkelijk snijpunten ontdekken die nog geen middelpunt zijn van een nieuwe cirkel en met dit gegeven kunnen ze ‘eindeloos’ verder.
Is het altijd nodig om de cirkel in z’n geheel te trekken. Wat als je maar een deel doet?
Dat komt in de tweede week aan bod.
Rudolf Steiner wijst met regelmaat op het feit dat het goed is wanneer kinderen ervaren dat de verschillende lesstof met elkaar te maken kan hebben. Omdat die samenhang er in de wereld – in het ‘echt’ is, haal je deze werkelijkheid de klas in en gaan de kinderen voelen dat er samenhang in de wereld is.
Zo zou je terug kunnen gaan naar de 5e klasperiode geschiedenis en wel naar Egypte. Je zal waarschijnlijk verteld hebben over de piramiden; over de bouw
ervan. Wie de grote wiskundigen waren die zo’n kolossaal bouwwerk wisten te ontwerpen.
In het boek van Strakosch vind je in de ‘Inleiding’ verwijzingen naar Egypte.
Deze inleiding is hier vertaald.
.
*Of ze ook gebruikt moeten worden voor het schrijven van de kleine drukletter (in het blokschrift). wordt hier besproken.
[1] De grote Rudolf Steiner citatensite
[2] K.Lapré: ‘De menselijke ziel’ -eigen uitgave -te bestellen via: kimlapre@gmail.com
[3] Over ‘spiegelen‘
[4] A.Strakosch ‘Geometrie durch übendes Anschauen‘, Mellinger Verlag, Stuttgart
In ‘De filosofie van de vrijheid’ heeft Steiner zeer waardevolle gezichtspunten gegeven over standpunt, waarnemen en denken.
GA 4
vertaald
**cirkel; liniaal; lineair; willekeurig; onwillekeurig; omtrek; middellijn; middelpunt, verticaal, horizontaal, diagonaal; vlak; snijden;
.
suggesties voor de periode:
6e klas: alle artikelen (waarbij de meetkunde-artikelen)
meetkunde: alle artikelen
VRIJESCHOOL in beeld: 6e klas- meetkunde: alle beelden
1113
.




































 4.Nardus
4.Nardus