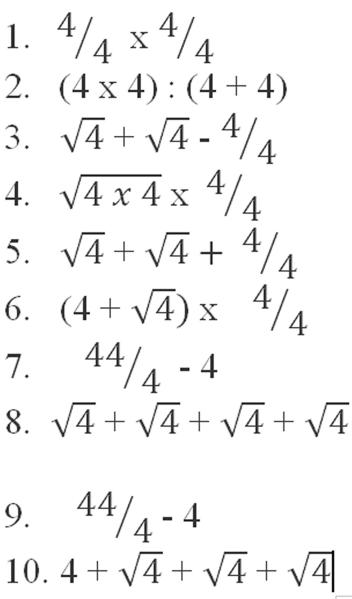VRIJESCHOOL – 6e, 7e en 8e klas – rekenen – rekenraadsels

Hieronder volgen rekenopgaven met een enigszins verrassend karakter.

Niet alle leerlingen zijn daarin geïnteresseerd, maar sommige wel en er zijn ogenblikken dat zij het heerlijk vinden om aan deze opgaven te werken; ook voor het ‘zeer begaafde’ kind kunnen ze een uitdaging betekenen.

[56]
NAAR DE OVERKANT

De scouts hebben een vlot gebouwd bij het meer. Op het vlot is er plek voor twee personen. Ze willen graag met het vlot ook de jongste groep (welpen) mee laten doen. Er kunnen twee personen op het vlot waarvan eentje moet roeien en alleen de oudere padvinders zijn sterk genoeg om te roeien. Maar daar worden ze wel moe van. Het oversteken kost ongeveer 15 minuten. Daarna moet de roeier minstens 15 minuten rust nemen.

Hoelang duurt het om met de hulp van 3 oudere scouts 3 welpen over het meer te zetten?

Oplossing:

We starten scouts 1 en 2 naar de overkant. De roeier (1) blijft achter en de andere (2) roeit terug. Nu gaat scout 3 met A naar de overkant en blijven daar. Daar staat 1 klaar die het vlot weer terugbrengt Nu gaat 2 roeien met B als passagier. A en B blijven aan de overkant wachten met 2 terwijl 3 weer oversteekt. Bij de start staat C nog samen met 1, die naar de overkant gaan. Dan zijn A, B en C over maar 2 gaat nog een keer naar de start om samen met 1 (die roeit) ook over te steken. In totaal gaat het 9 keer over het meer dus In totaal 2 uur en 15 minuten werk.

0-0-0

[55]
DATA

Een jaar geleden hadden we de datum 02-02-2000.
Zoals je ziet, een datum die uit alleen maar even getallen bestaat.
Dat is na het begin van onze jaartelling wel vaker voorgekomen.
Kun jij de datum vinden die als laatste – vóór 02-02-2000 – ook uit enkel even getallen bestond?
En als we vanaf nu – 10-07-2021 rekenen, wanneer is dan de eerstvolgende datum die dit ook vertoont?

Oplossing:

Enkel uit even getallen betekent dat alle data van 01-2000 t/m 12-900 niet in aanmerking komen. Het jaar 888 geeft pas mogelijkheden en daarvan als laatste de 8e maand met de 28e dag, dus 28-08-888.
De eerstkomende datum moet in 2022 vallen, ook in de 2e maand, de 2e dag.
Een vraag zou nog kunnen zijn: hoe vaak komt dat in die eeuw voor?

0-0-0

[54]
WAT KRIJG JE TERUG?

Je koopt bij een chocolaterie 500 gram bonbons. Er staat een mooi ingepakt doosje dat 18 euro kost. De bonbons zelf zijn 16 euro duurder dan de verpakking.
Je hebt niet al te veel spaargeld dus neem je de bonbons toch maar zonder cadeauverpakking; je krijgt ze mee in een gratis zakje. Je betaalt met een briefje van 20 euro. Wat krijg je terug?

Oplossing:

Een opdracht om goed te lezen. 18 euro is de prijs van bonbons + verpakking. Denk je dat de bonbons 16 euro kosten en de verpakking 2 euro? Dan zijn de bonbons 14 euro duurder dan de verpakking. In de opgave staat: “De bonbons zijn 16 euro duurder dan de verpakking.” Niet 14.
Het verschil van 2 is door de bonbons en de verpakking ontstaan. Beide zijn dus verantwoordelijk voor 1 euro. De bonbons kosten 17 euro, de verpakking 1. Je krijgt dus 3 euro terug.

Kunnen de leerlingen al met algebraïsche vergelijkingen werken, dan is dit een oplossing:

Noem de bonbons b en de verpakking v.
b + v = 18 euro
b = 18 euro – v (1)

b – v = 16 euro (2)

Combineer (1) en (2):
18 euro – v – v = 16 euro
2 euro = 2v
v = 1 euro
De bonbons kosten dus 18 – 1 = 17 euro.
En de verpakking kost 1 euro.

0-0-0

[53]
HOEVEEL TIJD NODIG? .

Twee klusjesmannen metselen ieder een identiek muurtje. De een heeft het in 2 uur af, de ander in 3 uur. Als ze met zijn tweeën één muurtje metselen in hetzelfde tempo, na hoeveel tijd is dat dan klaar?

Oplossing:

Een oplossing is te kijken naar de getallen 2 en 3. Als vermenigvuldiging zien we 6. Als de ene 6 uur metselt, heeft hij 3 muurtjes, de ander 2. In 6 uur hebben ze beide dus 5 muurtjes gemetseld. Over 1 muurtje doen ze dan samen 6 uur = 360 min.: 5 = 72 minuten. Ofwel 1.12 u

Of: De een doet per uur 1/2 muurtje en de ander doet per uur 1/3 deel. Met zijn tweeën doen ze in 1 uur 5/6 deel van het werk. Dan blijft nog 1/6 deel over. 5/6 deel in een uur = 1/6 deel in 1/5 uur = 1/6 deel in 12 minuten Dus 1 uur en 12 minuten

0-0-0

[52]
TOEREN TELLEN

Met onderstaande tandwieloverbrenging wordt een roerwerk aangedreven. De as waarop tandwiel 1 is gemonteerd, is de motoras. Deze as drijft via een tussenas de as van het roerwerk aan.
Tandwiel 1 op de motoras heeft 10 tanden. Op de tussenas zijn tandwiel 2 en 3 gemonteerd. Die hebben resp. 20 en 10 tanden.
Op de as van het roerwerk is tandwiel 4 gemonteerd. Dat tandwiel heeft 40 tanden.
Als het toerental van de motoras 1200 omwentelingen per minuut is, dan maakt het roerwerk hoeveel omwentelingen per minuut?

Deze afbeelding heeft een leeg alt-atribuut; de bestandsnaam is rekenraadsel-66-jpg..jpg

Oplossing:

Als de motoras [1] 1x rondgedraaid is, heeft hij as 2 voor de helft meegenomen, deze legt dus het halve aantal toeren van de motoras af= 1200 : 2 = 600. Als deze helemaal rond geweest is heeft hij ook as 3 een rondje laten draaien en deze beweegt met zijn 10 tanden er 10 voort van de roeras, dat is een kwart. Maar dat is dan ook een kwart van de 600 toeren die as 2 aflegt. Dus de roeras legt 600: 4 = 150 toeren af.

Of sneller:
1200 omw/min x 10 : 20 x 10 : 40 = 150 omw/min

[51]
HOEVEEL TREINEN ZIE JE TENMINSTE?

Elk half uur vertrekt in Maastricht een trein richting Amsterdam. De reis naar Amsterdam duurt 2 uur en 30 minuten. Uit Amsterdam vertrekt ook elk half uur een trein richting Maastricht.
Hoeveel treinen uit Amsterdam zie je tenminste gedurende die 2u en 30 minuten?

Oplossing:

In de 2u en 30 minuten kom je de treinen van elk half uur tegen die al vertrokken waren vóór dat jij afreisde; en terwijl jij in de trein zit vertrekken er nog eens 5, dat is dus samen 10. Maar op het moment dat jouw trein stopt, vertrekt de 11e. Het kan zijn dat de 11e net vertrekt als jij aankomt. Als dat op hetzelfde perron gebeurt, zie je er dus 11.

0-0-0

[50]
HOEVEEL KRALEN?

Een kind legt een hele sliert kralen achter elkaar.
Dan telt het vanaf het begin 47 kralen af en vervangt deze 47e kraal voor een rode. Dan begint het aan het einde van de sliert terug te tellen en – heel toevallig- is de rode kraal dan ook de 47e. Hoeveel kralen liggen er in die sliert?

Oplossing:

Als de 47e kraal voor een rode is vervangen, liggen er vóór die rode dan 46 kralen. Dat geldt ook voor ‘vanaf het einde’. Er zijn dus 2 x 46 kralen = 92 en de rode, zodat het antwoord 93 is.

0-0-0

[49]
DE SLAK OMHOOG

Onder aan een paal 30 centimeter hoog zit een slak. De slak klimt per minuut 3 centimeter. Daarna rust die slak 1 minuut uit en zakt daarbij 2 centimeter. Na hoeveel minuten is de slak boven aan de paal?

Oplossing:

Per minuut 3 cm stijgen, 1 min. rusten en 2 cm zakken, is een ‘bezigheid’ van 2 min. met een resultaat van 1 cm klimwinst. Je zou nu kunnen denken dat de slak bij 1 cm per 2 min. dus voor 30 cm 60 min. nodig heeft. Maar dan heb je bij de laatste klim ook weer gerekend met rusten en terugzakken. Dat gebeurt echter niet. als de slak op de paal zit, kan hij niet meer zakken.
Als hij 27 cm afgelegd heeft, kostte dat 27 x 2 min = 54 min. Dan komen de laatste 3 cm in 1 min. Dan is hij boven, dus na 55 min.

0-0-0

[48]
DE KERKKLOK SLAAT

Het is lekker weer en je wandelt door het centrum van je dorp. Het is 4 uur, dus slaat de kerkklok 4 keer. Je wil ‘zomaar’ weten hoe lang dat slaan duurt en je kijkt op je horloge: exact 3 seconden, van de eerste tot de laatste slag.
Nu komt ineens de vraag bij je op hoe lang het duurt als de klok 12 uur slaat.
Ja, hoe lang?

Oplossing:

Je zou denken: 4 slagen = 3 seconden, dan 12 slagen = 3x zoveel = 9 seconden.
Rekenkundig klopt dit wel, maar de realiteit is anders*, want de seconden kosten, hoe gek het ook klinkt voor leerlingen, ook tijd.
Hier kun je de getallenlijn gebruiken. Tussen slag 1 en 4 bevinden zich dan 3 ruimtes:
1___2___3___4
Als bij 4 slagen 3 seconden horen; op de getallenlijn 3 ruimtes, dan zijn er bij de getallen 1 t/m 12, 11 ruimtes, d.w.z. 11 seconden.

*zie realistisch rekenen

0-0-0

[47-1]
WELK GETAL KOMT IN HET GELE VAKJE?

De getallen in de blokken zijn telkens de som van de twee waarden eronder.
55 + ? = 73, 18. 18 + ? = 27 = 9.
41 + ? = 55, =14
14 + ? = 18, = 4
4 + ? = 9, = 5
27 + ? = 41, = 14
14 + ? = 14, = 0
0 + ? = 4, = 4
4 + ? = 5, = 1 = GELE VAKJE

0-0-0

Oplossing:

66 is de som van 41 + ? = 25; 34 is de som van 25 + ? = 9
41 is de som van 20 + ? = 21; 25 is de som van 21 + ? = 4
9 is de som van 4 + ? = 5; 20 is de som van 0 + ? = 20
21 is de som van 20 + ? = 1 4 is de som van 1 + ? = 3
5 is de som van 3 + ? = 2 =GELE VAKJE

0-0-0

[46-1]
REKENSTER

Oplossing:

Als het gaat om ‘gemiddelde’ moet er gedeeld kunnen worden; hier moet/kun je ook de andere rekenbewerkingen toepassen. Die zijn niet zo moeilijk, dus dat moet een 6e klas makkelijk kunnen.
Moeilijker is het begrijpen van de nogal abstract gestelde opdracht. Dus die moet je eerst ontrafelen. Dat kan het beste met het voorbeeld: 55 staat als gearceerde punt in vak D. Alle gearceerde punten moeten dus ergens op A t/m E komen te liggen. 55 is het gemiddelde van 3 getallen, t.w. 68, het getal dat in A en het getal dat in E komt = een zijde gemeenschappelijk.
Als 55 het gemiddelde is van 3 getallen, zijn deze samen 3 x 55 = 165. Je hebt al 68, dus voor de andere twee blijft 97 over. Dat zijn de getallen van A plus E, en dat zijn getallen uit de gearceerde reeks. Zie je daarbij 2 getallen die samen 97 zijn? Goed kijken en optellen: dat blijken 40 en 57 te zijn.
Stel dat A = 40, dan is dit het gemiddelde van weer 3 getallen, dus samen 120; daarvan heb je – aangrenzend al 73 en 55. Daar komt B nog bij. Dat is onmogelijk: 73 en 55 zijn al meer dan 120, dus A = 57.
Dat is het gemiddelde van 3 getallen, dus 171; daarvan heb je al 73 en 55 = 128. Het verschil is B = 43.
Op deze manier verdergaand geeft voor C: 28; voor F: 29

A = 57; B = 43; C = 28; D = 55; E = 40; F = 29

0-0-0

[46-2]
REKENSTER

Oplossing:

Als het gaat om ‘gemiddelde’ moet er gedeeld kunnen worden; hier moet/kun je ook de andere rekenbewerkingen toepassen. Die zijn niet zo moeilijk, dus dat moet een 6e klas makkelijk kunnen.
Moeilijker is het begrijpen van de nogal abstract gestelde opdracht. Dus die moet je eerst ontrafelen. Dat kan het beste met het voorbeeld: 28 staat als gearceerde punt in vak E. Alle gearceerde punten moeten dus ergens op A t/m E komen te liggen. 28 is het gemiddelde van 3 getallen, t.w. 2, het getal dat in D en het getal dat in F komt = de gemeenschappelijke zijden van E

Als 28 het gemiddelde is van 3 getallen, zijn die getallen samen 3 x 28 = 84. Een van de getallen is 2, de andere moeten samen 82 zijn. Welk tweetal van de gearceerde getallen is samen 82. Wanneer je ze allemaal op elkaar betrekt, zie je dat alleen 34 en 48 in aanmerking komen. We gaan er eerst vanuit dat D 34 is. Het is dus ook een gemiddelde, van 28, 78 en A. 3 x 34 = 102. D zou dan zijn: 102 – 28 -78. =minder dan 0, dus dit kan niet. Dan is D 48. F is dan 34 Die hebben we als gearceerde punt.
F = het gemiddelde van 28 en 23 en C. F = 34. 34 x 3 = 102. C = 102 – 28 – 23 = 51, ook dat is een gearceerde punt.
C= 51, het gemiddelde van B en F + 70. 3 x 51 = 153. B = 153 – 70 – 34 = 49, eveneens een gearceerde punt.
Voor A blijft de 38 over en bij narekenen klopt dat ook.

A = 38; B = 49; C = 51; D = 48; E = 28; F = 34

0-0-0

[46-3]
REKENSTER

Het is belangrijk dat leerlingen zo’n som kunnen lezen, kunnen ‘vertalen’ naar een hanteerbare manier om het vraagstuk op te lossen.

De ‘grijze’ vlakken zijn de donkere vlakken. Daar staat links beneden 64. Die is terechtgekomen in vak B. Zo moeten alle getallen in de donkere vlakken op de lichtere terechtkomen.
Er is een voorwaarde. Het getal – hier 64 – moet een gemiddelde zijn van de getallen die in de driehoeken staan waaraan B grenst. Hier dus A en C en een driehoek met het getal 97.
Een gemiddelde betekent dat je moet kunnen delen. Dan kan je daarvóór ook vermenigvuldigen. En wel 3 x 64 = 192. Dat is dus het gemiddelde van 97 + A + C. A + C zijn dan samen 192 – 97 = 95. Op de grijze punten moeten zich 2 getallen bevinden die samen 95 zijn. Dat zijn 53 en 42. Maar welke komt in A en welke in C. Door dat uit te proberen met bovenstaande ‘sleutel’ kun je ze allemaal vinden.

Oplossing:

In de uitleg waren A en C bijna bekend. Stel A – 53. Dan is dat het gemiddelde van 3 x 53 -( 64 + 47) Het antwoord is dan D, maar het moet wel in de grijze punten voorkomen: 48: en dat is een getal in een grijs vlak. Dus A = 53 en C 42
D moet nu zijn: 3 x 53 – (47 + 64) D = 48; E = 3 x 48 – (53 + 37) = E = 54
F moet nu zijn: 3 x 54 – (48 + 75 F = 39
Controle geeft C, want 3 x 42 = 64 + 39 + 23, dus alles is goed.

0-0-0

[46-4]
REKENSTER

Plaats de getallen uit de grijze vlakken op een zodanige wijze in de driehoeken A t/m F dat de waarde daarvan gelijk is aan het gemiddelde van de driehoeken waarmee ze een zijde gemeenschappelijk hebben. Eén getal is alvast ingevuld.

Die opgave oogt heel abstract. Het is dus allereerst de kunst zo te lezen dat je het begrijpt. ‘De getallen in de grijze vlakken’ spreekt voor zich: dat zijn 37, 63, 31, 49, 53 en 59. Op de een of andere manier moeten die verplaats worden naar de open driehoeken met de letters. Dat is met 53 gebeurd, die staat in A.
Driehoek A grenst aan driehoek D en B en daarmee heeft die dus een gemeenschappelijke zijde, maar ook met 79. De getallen van B en D weten we niet, maar wel dat het gemiddelde van driehoek 79, B en D, 53 is. Als het gemiddelde van 3 getallen 53 moet zijn, zijn de drie getallen samen 3 x 53 = 159. 1 getal hebben we al: 79, voor B en D samen blijven over 159 -79 = 80. Nu moeten we kijken naar de getallen in de donkere punten. Welke 2 zijn samen 80. Dat zij 31 en 49. Of B is 31, dan wel 49 of D is dat. Dat moet je uitproberen, dus bijv. je neemt voor B 31 en dan op bovenstaande manier kijken of het kan.
Daarna is het niet zo moeilijk meer.

Oplossing:

Als we voor B 31 nemen, is dit het gemiddelde van 3 getallen 3 x 31 = 93. Daarvan zijn 3 en 53 gegeven, dus moeten er voor C 37 overblijven: die hebben we in een donkere punt.
C= 37 als gemiddelde van 3 x 37 = 111, daarvan hebben we 31 en 17, waardoor er voor F 63 overblijft, die is er ook. 63 is het gemiddelde van E + 93 + 37 = 59. die klopt ook. D hoef je niet meer uit te rekenen, alleen 49 is over. Controle: 49 = het gemiddelde van 53 + 35 + 59 = 49!

A = 53; B = 31 C= 37 D = 49 E = 59 F = 63

[46-5]
REKENSTER

Die opgave oogt heel abstract. Het is dus allereerst de kunst zo te lezen dat je het begrijpt. ‘De getallen in de grijze vlakken’ spreekt voor zich: 56, 42,57, 63, 60, 71.
Het ingevulde getal is 71. Dit is het gemiddelde van de driehoeken die er aan grenzen B, F en 90. Als 71 het gemiddelde is van 3, dan is de som van die 3 getallen: 3 x 71 = 213. B + F zijn dan samen: 213 – 90 = 123. Zijn er nu 2 getallen in de grijze punten die samen 123 zijn. Dat zijn 60 en 63. Kan B 60 zijn: B is dan het gemiddelde van A + 52 + C(71), dus 3 x 60 = 180; we hebben al 52 en 71 = 123, blijft over 57. En die staat in een grijze punt, dus A = 57. Ga zo verder en vind de andere.

Nu we weten dat B = 60, is F 63; E is dan: 3 x 63 = 189 – (71 + 76) = 42 en dat is een grijs vlak.
E =42 en het gemiddelde van 7 en 63. 3 x 42 = 126. D = 126 – (7 + 63) = 56. En dat is ook een grijs vlak.
Blijft voor A over 57. Bij controle blijkt dat ook goed te zijn:
D is het gemiddelde van E = 42 en 69 en A. 3 x 56 = 168. A = 168 – (42 + 69) = 57 (is grijs vlak)

A = 57 B = 60 C = 71 D = 56 E = 42 F = 63

0-0-0

[45]
TANDWIELEN

In een torenklok grijpen twee tandwielen in elkaar.
Een groot tandwiel met 168 tanden en een klein tandwiel met 24 tanden. Op beide tandwielen staat een geel pijltje. Deze pijltjes wijzen nu precies naar elkaar.
Het kleine tandwiel verspringt ieder uur 1 tand.

Na hoeveel dagen wijzen de pijltjes weer precies naar elkaar?

Oplossing: het kleine tandwiel is na 24u helemaal rond gegaan, dat is 1 dag. Daarbij heeft het dus 24 tanden van het grote wiel verder geduwd.
Voor 168 tandwielen heeft het dus 168 : 24 = 7 dagen nodig. Dan is de beginstand met de pijltjes weer bereikt.

0-0-0

[44]
ALGEBRA EN/OF ANDERS?

Niet zozeer een ‘raadsel’, dan wel een som die een 8e-klasser? met behulp van algebra zou (moeten?) kunnen oplossen:

André koopt 3 boeken.
Boek A is 2 maal zo duur als boek C en 4/3 keer zo duur als boek B.
Boek B is 6 euro duurder dan boek C.
Hoe groot is het verschil tussen boek A en C

Oplossing:

Zijn de leerlingen in staat om bijv. boek C op verschillende manieren ‘te zien’: m.a.w. kunnen ze al vergelijkingen maken, zoals C = boek B minus 6 euro; of de helft van A; dan kan de volgende berekening ontstaan:

a = 2c (vergelijking 1)
a = 4/3 b (vergelijking 2)
c = b – 6 (vergelijking 3)

(1) en (2) combineren:
2c = 4/3 b
Dit combineren met (3):
2 x (b – 6) = 4/3 b
2b – 12 = 4/3 b
2b – 4/3 b = 12
2/3 b = 12
b = 18
Boek B kost 18 euro; boek C kost dan 12 en boek A 24 euro

Het verschil is dus € 12,–

0-0-0

[43]
KRAAK DE CODE

Oplossing:

De vermenigvuldiging kan al voor iets zorgen: B = 1, E dan 6 of omgekeerd of B = 2, E 3 of omgekeerd. Deze mogelijkheden gaan we na bij andere combinaties: Door E – D=2, kan E geen 1 zijn; door C – B= 3 kan B geen 6 zijn; als B = 1, dan E = 6; in E – D = 2, is D 4. Maar 6 is even en er zit maar één even getal bij. E valt ook af als 6; dan kan B ook geen 1 zijn.

Blijven voor B en E 2 of 3 over. Als B 3 is, is in C – B = 3, C 6. Maar E is al even, dus dat kan niet. B is dus 2 en E is 3.

In A + B = 5, is A 3; in E – D = 2, is D 1; in C – B = 3, is C 5; in E + F = 6, is F 3

A = 3 B = 2 C = 5 D = 1 E = 3 F = 3

0-0-0

Oplossing:

Er zijn geen vermenigvuldigingen die meestal wel al een zeker getal opleveren. Nu zullen we de aanwijzing moeten gebruiken dat er 1 oneven cijfer in zit.
Het cijfer 8 kan alleen opgebouwd worden uit: 2 + 6, 4 + 4 en 3 + 5. Voor 3 + 5 zijn twee oneven getallen nodig, dus blijft 2 + 6 over. Datzelfde geldt voor E + F.
Uit E – D = 3 blijkt dat E geen 2 kan zijn, dus is of 4 of 6. Uit C – E blijkt dat E geen 6 kan zijn (C zou dan 8 zijn en dit cijfer doet niet mee), E is dus 4, waaruit volgt dat C = 6. Uit E – D = 3 volgt dat D = 1
Uit B + C = 8 volgt dat B = 2; en A is dan 4; F blijkt dan 4 te zijn.

A = 4 B = 2 C = 6 D = 1 E = 4 F = 4

0-0-0

Oplossing:

Vermenigvuldigen kan alleen met bepaalde factoren: hier, bij E x F = 6 kan het alleen om 2,3, 1,6 gaan. Uit B – E volgt, dat E geen 6 kan zijn, dus F geen 1, wel kan E 1 zijn en F 6; blijven 2 of 3.
Uit B – D = 5 valt af te leiden dat B alleen 5 of 6 kan zijn. Dan kan E geen 1 zijn en dus F geen 6, blijven 2 en 3. Als B =5, dan E = 2; dan C= 1; D=0; A= 4, dan echter is A + D geen 5, B moet dus 6 zijn. C = 0; D = 1; A = 5; E = 3 en F = 2

Dus: A= 5; B = 6; C =0; D = 1; E =3; F = 2

0-0-0

Oplossing:

Nu er geen vermenigvuldiging in zit, hebben we geen vaste cijfers en moeten we wat proberen. In B + E = 10 kan B alleen 4 of 6 zijn. In A + B = 5 kan B geen 6 zijn, dus is B 4 en A 1; E = 6; C =4; D = 3; F = 2

A = 1; B = 4; C = 4; D = 3; E = 6; F = 2

0-0-0

Oplossing:

Geen vermenigvuldiging, maar A + C = 11 geeft al aan dat A en/of C 5 of 6 zijn. Daarmee kunnen we verder proberen: Stel: A = 5: C is dan 6 en in A + C + D = 15, is D dan 4; in C + D + E = 15, is E dan 5; A + E moet dan 10 zijn en dat klopt.
in E + F = 6, is F dan 1 en in A + B + F = 8, is B 2.

A = 5; B = 2; C = 6; D = 4; E = 5; F = 1

0-0-0

Oplossing:

De vermenigvuldigingen geven ons houvast: bij D x F = 6 zijn D en F geen 4 of 5; datzelfde geldt voor B x C. Er zit geen 4 in. In E + F = 11 is E of 5 dan wel 6, wat ook voor F geldt. F kan echter geen 5 zijn, dus F = 6 en E is dan 5. D is 1 en daarom A 5, B is dan 3 en C 2.

A = 5; B = 3; C = 2; D = 1; E = 5; F = 6

0-0-0

Oplossing:

Vermenigvuldigen geeft vaste cijfers. In B x C = 5, zijn B en C 1 of 5.
We zullen nu van iets moeten uitgaan: stel B = 5, komen we dan verder. Niet direct, we weten nu alleen dat in A + B + D = 5, A + D 0 zijn. Als A = 0, dan is E 4 en F = 2. Maar D + E + F moet 10 zijn, maar het is 6, dus B kan geen 5 zijn. Dan is B 1 en C =5.
Bij B = 1 komen we niet snel verder, want we weten alleen dat A + D dan samen 4 zijn; in A + F = 2, kan A alleen 0, 1 of 2 zijn.
Gaan we uit van A = 0, dan is E 4 en F 2: E + F zouden dan samen 6 zijn en dat zijn ze!
In D + E + F = 10 is D dan 4. Toen we A = 0 namen, hadden we B al als 1, dus D was daar 4. Langs de andere weg vonden we D – 4 ook al, dus alles klopt.

A = 0; B = 1; C = 5; D = 4; E = 4; F = 2

0-0-0

Oplossing:

Geen vermenigvuldiging, maar in A + F = 0, zijn A en F 0; daarmee verder: in A + B + F = 3, B = 3; in B + C + E = 3; C + E = 3, dan zou C en/of E 0 of 3 zijn. 3 is oneven en er staat dat de som van alle oneven cijfers 3 is. Maar we hebben al een 3, dus C en/of E zijn geen 3, maar 0. In B + D + E = 5 is D 2.

A =0; B = 3; C = 0; D = 2; E = 0; F = 0

0-0-0

Oplossing:

A x C geeft ons al de waarde van A en C, nl. 1; daarmee verder gezocht: A + B + C = 3: B = 1; A + B + F = 6: F = 4; B + D = 6, D = 5; A + D + E = 8: E = 2.

A = 1; B = 1; C = 1; D = 5; E = 2; F = 4

0-0-0

Oplossing:

A x E = 10, dus A en/of E zijn 2 of 5; als A = 2, dan in A + B + F = 15 zijn B + F samen 13, daarvoor is een 7 nodig en die doet niet mee. Dus A = 5; E = 2; daarmee verder: B + E = 7, B = 5; in B + C = 7, C = 2; in C + D = 4: D = 2; in A + B + F = 15: F = 5

A =5; B = 5; C 2; D = 2; E = 2; F = 5

0-0-0

Oplossing:

De vermenigvuldigingen geven vaste cijfers: in B x C = 15, zijn B en/of C 3 of 5; in A x C = 12, kan C geen geen 5 zijn, dus is deze 3; daarmee weet je B = 5; A = 4; daarmee kun je verder: B + D = 8: D = 3; A + E = 10: E = 6; A + D + F = 11: F = 4

A = 4; B = 5; C = 3; D = 3; E = 6; F = 4

0-0-0

Oplossing:

Begin met de vermenigvuldiging: die levert vaste cijfers op: C x D = 8. Dan kunnen C en D 2 of 4 zijn. Daarmee gaan we zoeken: D + E = 9. Bij D = 2, zou E 7 moeten zijn, maar de 7 doet niet mee, dus is D 4 en dan C 2, E is dan 5. Daarmee kunnen we verder: C + E + F = 13: F= 6; A + D + F= 12: A = 2; dan B = 1

A =2; B = 1; C = 2; D = 4; E = 5; F = 6

0-0-0

Oplossing:

Vermenigvuldigen geeft vaste cijfers: B x D = 6; dan kunnen die 1, 2, 3 en 6 zijn. In D + E = 4 kan D geen 6 zijn; dan is B niet 1; in B + C = 4 kan B geen 6 zijn, dus D geen 1; dan moeten we iets proberen: stel B = 2, dan is C 2; in A – C = 3 zou A 5 moeten zijn, maar er wordt gezegd dat er geen 5 in zit. Dus B is geen 2. Dan blijft voor B 3 over. C is dan 1; A dan 4 en F = 1; D is 2 en E dan ook 2.

A = 4; B = 3; C = 1; D = 2; E = 2; F = 1

0-0-0

Oplossing:

Vermenigvuldigen geeft vaste cijfers: in A x B = 4, is A en/of B 1, 2, 4. 2 valt af: die zit niet in de combinatie. In B x F = 6 kan B geen 4 zijn, dus is deze 1 en F is dan 6, A =4; in F – E = 4 is E dan 1 en dan is in D x E = 6, D 6. In C- B = 2, is C 3.

A = 4; B = 1; C = 3; D = 6; E = 1; F = 6

0-0-0

Oplossing:

De vermenigvuldigingen geven vaste getallen. In A x C = 6, is A en/of C 1, 2, 3, 6.
In D x E = 3, zijn D en E 1 of 3.
Als we D = 3 nemen, moet in C + D, C 0 zijn, maar de aanwijzing is verder dat er geen 0 in de code zit. D kan geen 3 zijn en is dus 1, E = 3. In C+ D = 3, is C dan 2. In D + F = 6, is F dan 5. In B+ C = 8, is B 6; en in A x C = 6, is A 3.

A = 3 ; B = 6; C = 2; D = 1; E = 3; F = 5

0-0-0

Oplossing:

Vermenigvuldigen geeft vaste cijfers: in B x D = 10, is B en/of D 2 of 5. We proberen: stel B = 2, dan is F in B + F = 6, 4. Maar in E x F = 6, kan F geen 4 zijn, dus is B geen 2, maar 5; D = 2; in B – C = 2, is C dan 3; in B + F = 6 is F 1; C = 3, dan A = 2; E = 6.

A = 2; B =5; C = 3; D =2; E 6; F = 1

0-0-0

Oplossing:

De vermenigvuldiging A x C = 10 geeft ons dat A of C 2 of 5 zijn. In C + F = 3 kan C alleen maar 2 zijn, dan is A 5; F is dan 1; B is dan 0; in C + D + F = 8 is D dan 5; in A + E + F = 7 is E 1
A = 5; B = 0; C = 2; D = 5; E = 1; F = 1

0-0-0

Oplossing:

Vermenigvuldigen levert vaste getallen. In A x D = 6, kunnen A en D 1, 2, 3 of 6 zijn, maar er komt – aanwijzing – geen 1 in de oplossing voor, dus die valt weg en A en/of D kan geen 6 zijn, dus 2 of 3.
We kiezen A = 2. Dan is in A + B = 8, B 6; in B + C = 6, is C dan 0; door de keuze van A = 2, is D 3; in D – F = 0, is F dan 3; en daardoor is in E – F =1, E 4.
Dat blijkt allemaal te kunnen, dus de keuze voor A = 2, was meteen raak.

A = 2 B = 6 C = 0 D = 3 E = 4 F = 3

0-0-0

Oplossing:

Nu er geen vermenigvuldiging in zit, moet je iets ‘willekeurigs proberen, ’t liefst met zo min mogelijk mogelijkheden. Bij F – E = 4 kan F alleen 5 of 6 zijn, E alleen dan 1 of 2, in dit geval kunnen we alleen verder zoeken met E in D + E = 6. Nu is het een zaak van alle mogelijkheden nalopen. Uiteindelijk blijkt B geen 3 te kunnen zijn, maar 4; daarom is C 3; D 4 en E 2, dan is F 6.

A = 1 B = 4 C = 3 D = 4 E = 2 F = 6

0-0-0

Oplossing:

De vermenigvuldiging C x E levert voor C en E 3 of 5 op.
Er zijn geen bijzondere aanwijzingen, dus zullen we moeten proberen.
Eerst maar C= 3; dan C – B = 3, B = 0; B + D =4, dan D 4; D + E = 5, dan E = 1. Maar E is 3 of 5, dus C = geen 3, dan 5 en E is 3.
In C- B = 3 = B 2; in F- E = 3 F = 6; in D + E = 5: D= 2; in A – B = 2: A =4;

A = 4; B = 2; C =5; D = 2; E = 3; F = 6

0-0-0

Oplossing:

Het is altijd slim om eerst met de vermenigvuldiging(en) te beginnen: daarbij liggen cijfers vast, zoals hier: B x F = 12 , dan B en/of F 2, 6, 3, 4
Nu gaat het erom cijfers te kunnen uitsluiten.
Stel B = 2, dan F = 6; verdergaand met deze cijfers: B + D = 7: D = 5; A + D = 5. dan A = 0; B – A = 2: 2 – 2= 0, tot nog toe klopt het; C – D = 5: Nu zou C 10 moeten zijn, maar die doet niet mee. Poging mislukt.
Stel B = 6, dan F 2; B + D = 7: D =1; B – A = 2: A = 4; A + D = 5: D = 1
C – D = 5: C = 6; C + E = 6: E =0
Deze klopt.
A = 4; B = 6; C = 6; D = 1; E = 0; F = 2

0-0-0

Oplossing:

Vermenigvuldigen levert vaste cijfers op, zoals hier in B x E = 6. Beide kunnen 1, 6, 2 of 3 zijn. In E + F = 5, kan E geen 6 zijn, daarmee B geen 1.
Wat als B = 6, dan in B + D = 8 = D 2, dan is A 3; E is dan 1; F = dan 4 en C 4; bij C + D klopt dit. Ook klopt C + F = 8 dan. Dus:

A = 3; B = 6; C = 4; D = 2; E = 1; F = 4

0-0-0

Oplossing:

De vermenigvuldiging kan ons op weg helpen: A x F = 12, dan A en/of F 2, 3, 4, 6.
In E + F = 9, kan F geen 2 zijn, want 7 doet niet mee. Daarmee valt ook 6 weg. A en F zijn dus 3 of 4. Nu moeten we wat uitproberen. Stel A = 3, dan volgen C = 3, F = 4; E = 5; in A + B = E = 13, zou B dan 5 zijn. Door B + D = 9, zou D 4 moeten zijn; en B + C + D 11, maar B + C + D = aangenomen: 5 + 3 + 4 = 12. Het uitgangspunt A = 3, is dus verkeerd, dan is A 4 en F 3; E is dan 6; B = 3; D dan 6; C = 2. Bij controle klopt alles.

A = 4; B = 3; C = 2; D = 6; E = 6; F = 3

0-0-0

Oplossing:

Deze keer geen vermenigvuldiging in de opgave: dat maakt het vinden iets lastiger. Omdat we weten dat 7, 8 en 9 niet meedoen, kan bij C + D = 11, alleen de 5 en de 6. We kunnen niet anders dan hiermee proberen. Eerst maar C = 5 en dan zien hoe ver we komen. Dan is in B + C = 9. B 4, E zou dan 3 zijn, F 5, A 2, D 6. Dat blijkt bij controle goed te zijn:

A = 2; B = 4; C = 5; D = 6; E = 3; F = 5

0-0-0

Oplossing:

Vermenigvuldigen helpt je aan vaste cijfers: E x F = 0, dus een van de twee is 0. In D x E – 12, kan E geen 0 zijn, dus is F 0. In A + F = 3, is A dan 3; in C + F = 3 is C dan 3; in A + C + D = D dan 2; dan is E 6 en in B + E = 11 is B 5.

A = 3; B = 5; C = 3; D = 2; E = 6; F = 0

0-0-0

Vermenigvuldig levert vaste cijfers: B x D = 4, dan B en D 1, 2 of 4
A x D = 2, dan A en D 1 of 2: D kan geen 4 zijn, B kan dan geen 1 zijn. Alleen een 4 of een 2.
Met deze gegevens moeten we iets proberen.
In B + F = 9 kan B geen 2 zijn, want F is dan 7 en die zit er niet in. Dus B = 4, dan D = 1 en A = 2. F is dan 5, E is dan 1; C dan 1.

A = 2; B = 4; C = 1; D = 1; E = 1; F = 5

0-0-0

Oplossing:

Vermenigvuldigen levert vaststaande getallen op, bv. in C x F = 2, is C of 1, of 2, wat ook voor F geldt.
Neem C als 1, dan kan het gegeven D + C = 8 niet, omdat D dan 7 zou moeten zijn en die zit er niet bij: C = dus 2, F = 1 en D = 6.
D x E = 6: E = 1. B + E = 4: B = 3; B – A = 1: A = 2

0-0-0

Oplossing:

Vermenigvuldigen geeft ‘vaste’ getallen: B x D = 4: B = 1,2 of 4, ook zo voor D. In C x E = 5, is C 1 of 5, idem voor E.
Nu moeten we een keuze maken. Stel B = 1 en E = 1, dan zou in A + B + E = 10, A 8 zijn, maar 8 doet niet mee. Dus gaan we nu E = 5 proberen. In A + B + E zou A dan 4 zijn. Maar in A + B + F = 14, zou F dan 9 zijn en die doet ook niet mee.
Dan proberen we de combinatie B = 4 en E = 1. In A + B + E = 10, dan is A 5, in A + B + F = 14 is F dan 5. Voorlopig kan dit. Bij E = 5, is in C + D + E = 7, is E 5, maar door die keuze is C 1 en daarom D 1. We hebben nu voorlopig A = 5; B = 4, C = 1, D = 1, E = 5 en F = 5. We voldoen hiermee ook aan de eis dat er 5 oneven getallen in de code zitten. We hebben het probleem hiermee opgelost:

A = 5; B = 4, C = 1; D = 1; E = 5; F = 5

0-0-0

Oplossing:

Vermenigvuldigen geeft vaste cijfers:

C x E = 15; dan C en/of E 3 of 5. In B x D = 5: B en/of D 1 of 5.
Wat voor (on)mogelijkheden doen zich voor met deze gegevens. Als we in D + E = 6, E de mogelijkheid 3 geven, dan is D 3, maar D is 1 of 5, dus E kan geen 3 zijn, dan is E 5 en C = 3; en D 1, dus B = 5; dan zie je al in A + C + E = 12, dat A 4 moet zijn. Dan is F 6;

A = 4; B = 5; C = 3; D = 1; E = 5; F = 6

0-0-0

Oplossing:

Het is altijd verstandig om met de vermenigvuldiging(en) te beginnen: dat levert vaststaande getallen op: hier B x D = 6: B, D zijn 1, 6 2, 3. We kunnen systematisch met B beginnen en kijken welke getalen (niet) kunnen. Uit B + C + F = 3 blijkt dat B geen 6 kan zijn.
Als B = 1, dan in B – C = 1, is C 0. In B + C + F = F dan 2; in D – F = 3 zou D dan 5 moeten zijn en dat kan niet: geen deler van 1 x 6 of 2x 3.
Daaruit volgt dat B ook geen 1 kan zijn.
Als B = 2, dan in B – C =1 is C 1. In B + C + F = F dan 0; in D – F = 3 zou D dan 3 zijn. Dat kan.
Ter controle nemen we B = 3. dan in B + C + F = 3, zijn C en F 0; dat F 0 ia, dan kan, maar in B – C = 1, waarbij B 3 is en C 0, kan dit niet.

B is dus 2 en D is dan 3. A is dan 4; C is 1; in B + E = 6 is E 4

A = 4; B is 2; C = 1; D = 3; E – 4; F = 0

0-0-0

Oplossing:

Vermenigvuldigen geeft vaste cijfers: B x E = 3: dan B en/of E 1 of 3; in B x D = 18 kan B geen 1 zijn, dus is B 3, E dan 1 en D 6; dan is A 3; C: 3 en F =2

A = 3 B = 3 C = 3 D = 6 E = 1 F= 2

0-0-0

Oplossing:

De vermenigvuldiging leert ons dat B en/of F = 1 of 2. Nu moeten we maar iets proberen: we nemen B = 1. In B + C = 5 is C dan 4 met als gevolg dat in C = F = 4 F 0 is. Maar F is 1 of 2. B kan dus geen 1 zijn, dan 2 en F is 1. C = dan 3; in C + E = 9 is E 6; in C + D + E = 11 is D 2. In A + B + E = A 4

A = 4 B = 2 C = 3 D = 2 E = 6 F = 1

0-0-0

Oplossing:

Vermenigvuldigen levert vaste cijfers. C x F = 12: C = 2, 3, 4, 6, dat geldt ook voor F. In E + F = 9 kan F geen 2 (E is dan 7, maar die doet niet mee), Als F 3 is, is E in E + F = 9, 6, maar dat kan niet in C + E = 5, F is dus ook geen 3. Als F geen 2 of 3 kan zijn, kan C geen 6 of 4 zijn.
Als we voor C 2 nemen, is F 6. In E + F = 9, is E dan 3 en in C = 2 + E = 3 =5, klopt dat. Dan is in C + D = 3, D 1 en daaruit volgt dat B = 5, en A = 3.

A = 3; B = 5; C = 2; D = 1; E =3; F = 6

0-0-0

Oplossing:

Vermenigvuldigen geeft vaste cijfers, dus in A x E = 12 zijn A en/of E 2,3,4 of 6. We zien A en E nog een keer, dan zijn ze samen 8; dat kan alleen met 2 en 6, dus 3 en 4 vallen af. Uit A + D + E = 10 volgt nu, dat D = 2; in C + D = 5, dat C = 3; in C + E + F = 6, kan E dan geen 6 zijn, dus E = 2 en A =, 6.
F = 1; in B + C + D = 10, is B dan 5

A = 6; B =5; C = 3; D = 2; E = 2; F = 1

0-0-0

Oplossing:

Omdat je vermenigvuldigingen hebt, heb je ook al bepaalde cijfers:

In B x D = 10 zijn B en D of 2 of 5. In B x E = 6 kan B geen 5 zijn, dus is deze 2
Dan weet je ook meteen dat D 5 is en E 3. Dan is C 1; A is dan 4 en F is 1

A = 4; B = 2; C = 1; D = 5; E = 3; F = 1

0-0-0

Soms is er geen andere mogelijkheid dan de onmogelijkheden systematisch op te sporen. Er is maar 1 vermenigvuldiging en die levert als antwoord in ieder geval op dat E of F = 0, of ze hebben de waarde van 1 t/m 6. F kunnen we nergens meer uitproberen, dus blijft E over. Als we die 0 nemen, zijn in A + B + E = 12, A + B 12, dus A = dan 6 en B ook.

Dan verder met A: in A + D = 8, is D dan 2, zo verder zoekend: C = 4, maar dan in B – C = 1, moet B 5 zijn en we waren uitgegaan van B = 6.

Conclusie: E is geen 0, dan is F 0.
Nemen we nu E = 1, dan is A + B 11, dus 5 of 6 of 6 of 5. We zagen al dat als we A 6 nemen, B 5 wordt. Nu verder controleren en alles blijkt te kloppen:

A = 6; B = 5; C = 4; D = 2; E = 1; F = 0

0-0-0

Oplossing:

De vermenigvuldiging geeft je vaste cijfers. In A x E= 3 zijn A en E 1 of 3.
Met deze gegevens verder zoeken: F – E = 5: zou E 3 zijn, dan F 8. Maar 8 doet niet mee, dus is E 1 en A 3. F = 6; D dan 6; B dan 5; C= 4

A = 3 B = 5 C = 4 D = 6 E = 1 F = 6

0-0-0

Oplossing:

Er is 1 vermenigvuldiging en die geeft ons 4 mogelijkheden: B = 1, 2, 3 of 6, wat ook geldt voor D. D kan geen 6 zijn in C + D + A = 7, dan kan B geen 1 zijn en blijven 2 en 3 over. Stel B = 2, dan is C in B – C = 1 1. Maar in C + E = 6, zou E, wanneer C 1 is, 5 zijn en die komt – gegeven – niet in de combinatie voor. B kan dus geen 2 zijn en is daarom dan 3. C = 2. D = dan 2. A = 3. E = 4; F = 1

A = 3; B – 3; C = 2; D = 2; E = 4; F = 1

0-0-0

Oplossing:

We hebben geen vermenigvuldiging(en) waardoor we ook geen ‘vaste’ cijfers hebben. We dus naar iets opvallends zoeken, zoals E + F = 1, want daarbij is of E 0, of F. We nemen E = 0. Dan lopen we vast bij D + E = 7, want D zou dan 7 moeten zijn, maar dat getal doet niet mee. Dus is E 1. Dan is F 0 en D = 6; die getallen toepassend geeft: B =2; A = 4; C = 6

A = 4; B = 2; C = 6′; D = 6; E = 1; F = 0

0-0-0

Oplossing:

Vermenigvuldigen geeft vaste cijfers. In B x D = 6, zijn B en/of D 1, 2, 3, 6. Daarmee moeten we logisch proberen. B kan geen 6 zijn in B – D = 1, D zou dan 5 moeten zijn, maar die zit niet in de combinatie. D kan dan geen 1 zijn. D kan ook geen 6 zijn in D – F = 1; dan blijven 2 en 3 over. Stel D = 2, dan is F 1; B is dan 3 en daardoor C 2 en E 4; A is daardoor 3. Bij controle blijkt de keus stel D = 2, juist te zijn.

A = 3; B = 3; C = 2; D = 2; E = 4; F = 1

0-0-0

Oplossing:

De vermenigvuldiging B x C = 6 houdt in dat B en/of C 1, 2, 3 en 6 kunnen zijn. In C + E = 9 kan C geen 1 of 2 zijn: 7 en 8 doen niet mee. wat betekent dat B geen 6 of 3 kan zijn. Laten we proberen met C = 3; in C + E = 9 zou E dan 6 zijn, maar A + E =4, dan kan E geen 6 en dus C geen 3 zijn. Dan blijft voor C =6. B = 1; E = 3; A = 1; als B = 1, blijven voor D + F 12 over: dan zijn zij allebei 6.

A = 1; B = 1; C = 6; D = 6; E = 3; F = 6

0-0-0

Oplossing:

Er is geen vermenigvuldiging, dus we hebben om te beginnen geen vaste cijfers. We moeten dus logisch proberen. Bv. E + F = 1, dan is E en/of F 1 of 0. In D + E = 7, kan E geen 0 zijn, want 7 zit niet in de combinatie. Dan is E 1; F = 0; gaan we verder met E = 1; in B + E = 3, is B dan 2; in D + E = 7, D = 6; verder invullend: D = 6; A = 4; C = 6

A = 4; B = 2; C = 6; D = 6; E = 1; F = 0

0-0-0

Oplossing:

Begin met de vermenigvuldiging: dan heb je vaste getallen. Omdat de 8 niet meedoet, is D x E =16: D = 4; E = 4. Die zijn samen u, dus moet A 3 zijn. C is dan 6;. B = 2.; F = 3.
A = 3; B = 2; C = 6; D = 4; E = 4; F = 3

0-0-0

Oplossing:

Vermenigvuldigingen leveren vaste cijfers op, dus eerst kijken we naar B x E = 6 en D x E = 8. Die hebben iets gemeenschappelijks: E
E kan zijn: 1, 2, 3 en 2, 4. De 2 is gemeenschappelijk, dus E = 2, B dan 3 en D = 4. Bij C – B = 3, is B 3, dus C = 6; in C + F = 8, is F dan 2; in A + D = 9 is D 4, dus A = 5

A = 5; B = 3; C = 6; D = 4; E = 2; F = 2

0-0-0

Oplossing:

We zoeken eerst weer de vermenigvuldigingen uit: C x D = 4: dan zijn C en/of D 1, 2 of 4.
Daar kunnen we in eerste instantie niets mee. In B x F = 8 zijn B en/of F 2 of 4. In A + F = 3 kan F geen 4 zijn, dus 2 en A dan 1, B is 4. In B + E = 10 is E dan 6. In A + D + E = 8 is D 1, dan C 4.

A = 1 B = 4 C = 4 D = 1 E = 6 F = 2

0-0-0

Oplossing:

Vermenigvuldigen geeft vaste getallen. D x E = 15: D en E zijn 3 of 5. In C x D = 10, kan D alleen 5 zijn; E is dan 3 en C = 2; in A x E = 0 is A 0; door A + B + E = 6 weten we dat B is 3; en bij B + F = 8, is F 5.

A = 0 B = 3 C =2 D = 5 E = 3 F = 5

0-0-0

Zoek de 6-cijferige code met behulp van onderstaande aanwijzingen. De cvijfers kunnen variëren van 0 t/m 6. Er komt dus nooit eren 7, 8 of 9 in de code voor.

Oplossing:

Een vermenigvuldiging beperkt het aantal mogelijkheden. A en E kunnen alleen 2 en 6 of 3 en 4 zijn.
D + B = 7 heeft als gevolg dat D geen 0 kan zijn, dus A kan geen 6 zijn. E kan dan geen 2 zijn. A kan wel 2 zijn, 3 of 4.
Stel A = 3; dan is E 4; D 3 in A + D; en B= 4 in D + B; dan is F 3 in F+ B; C = 2 in F + C; maar met de gevonden getallen is C + E 6 i.p.v. 7; dus A kan geen 3 zijn.

Ook als je A = 4 neemt, loop je vast. Dus A moet wel 2 zijn:
E=6; C is dan 1; F= 4; B = 3; D = 4 dus:

A = 2; B = 3; C = 1; D = 4; E = 6; F = 4

0-0-0

KRAAK DE CODE

Oplossing:

Er zijn vermenigvuldigingen, dus we hebben een paar vaste cijfers: in A x F = 24 is A en F 4 of 6, dat geldt ook voor B en F; en in B x E = 4 is B en E 1 of 4; maar hier valt 1 voor B weg, omdat B 4 of 6 is, in dit geval dus 4. Dan hebben nu ook A al: 4 en F = 6 en E is 1. In D + E = 3, is D dan 2; in A + C + D = 11 moet C dan 5 zijn.

A = 4; B = 4; C = 5; D = 2; E = 1; F = 6

0-0-0

Oplossing:

Het is (meestal) belangrijk om de vermenigvuldigingen eerst te bekijken, omdat daar de cijfers veel vaster liggen, hier bijv. C x F = 6. Dan kunnen deze of 1 en 6 of 2 en 3 zijn, andere getallen zijn uitgesloten.
Uit C – B = 2 blijkt dat C geen 1 kan zijn. Wat kunnen we nog meer van C te weten komen? Uit C + E = 3 volgt, dat C geen 6 kan zijn. Dan blijven 2 en 3 over. Omdat er geen andere vermenigvuldigingen meer zijn, en F nergens anders voorkomt, moeten we met C als 2 of 3 verder gaan zoeken.

Eerst maar: stel C = 2; dan is in C + E = 3 E 1, B in C + B = 2 0; dan is in B + D =6 D = 6; in D + E = 7 klopt wat we tot nog toe gevonden hebben.
In A + B = 6, A = 6; F was al 3
De keuze C = 2 blijkt meteen goed te zijn.
Als je van C = 3 uitgaat, loop je vast (C + E = 3 E= 0, maar in D + E = 7 moet E minimaal 1 zijn)

Dus: A = 6; B = 0; C = 2; D = 6; E = 1; F = 3

0-0-0

Oplossing:

Het blijkt steeds dat de vermenigvuldiging sneller tot een antwoord leidt dan bijv. een optelling. E x B = 3: E = 1 of 3; B = 1 of 3. De andere vermenigvuldiging helpt niet mee: C x F = 0, kan alles zijn, waarbij C = 0 of F = 0. Omdat C + B = 4 en B hooguit 3 kan zijn, kan C nooit 0 zijn, dus is F 0.In A + F = 6 is A dus 6; in A + D = 10 is D dan 4; in D + E = 7 is E dan 3, dan B = 1; in C + B = 4 is C dan 3

A = 6; B = 1; C =3; D= 4; E= 3; F=0

0-0-0

Oplossing:

Vermenigvuldigen geeft vaste cijfers: in E x F = 12, komen 2, 3, 4, en 6 in aanmerking; in C x F = 18: 3 en 6, waaruit volgt dat F = 3 of 6; stel F = 6, dan C = 3; E = 2; D = 6; B = 0, dan moeten A + B + F 6 zijn, A is dan ook 0. Bij controle klopt dus F = 6

A = 0; B = 0; C = 3; D = 6; E = 2; F = 6

0-0-0

Oplossing:

Vermenigvuldigen geeft vaste cijfers: B x F = 4: B en F zijn of 1, 2, 4; uit D + F = 2 volgt dat F geen 4 kan zijn, dan is B geen 1. Uit A + B = 2 volgt dat B geen 4 kan zijn, dus F geen 1, blijven voor beide 2 over. Dan zijn A en D allebei 0; C is dan 1; uit B + D + E = 7 volgt dan dat E = 5.

A =0 B = 2 C = 1 D = 0 E = 5 F = 2

0-0-0

Oplossing:

Vermenigvuldigen geeft houvast: D x E = 10: D = 2 of 5; E idem.
C x D = 6 C = 1 of 6 of 2 of 3; maar D kan hier alleen 2 zijn.
D = 2; E = 5; C = 3.
Met deze gegevens verder: C – B = 1. C = 3, dus B = 2.
F – B = 2, dus F = 4; A + C = 4, dus A = 1;
A = 1 B = 2 C = 3 D = 2 E = 5 F = 4

0-0-0

Oplossing:

Vermenigvuldigen geeft vaste cijfers: in D x F = 0 is D of F 0; maar in C x D = 15, kan D geen 0 zijn, dus is F 0.
In C x D = 15 zijn C en/of D 3 of 5; in A + C + D = 11, wetend dat C + D 8 is, is A 3. In A + E + F = 6 zijn A + F 3, dus E = 3; in A + D + E = 9 zijn A + E 6, dus D = 3; dan is in C x D = 15, C 5; in B + E + F = 9 is E + E 3, dus B = 6

A = 3; B = 6; C = 5; D = 3; E = 3; F = 0

0-0-0

Oplossing:

Wanneer je met de vermenigvuldigingen begint, kom je al snel tot antwoorden: de (vermenigvuldig)getallen liggen vrij vast, zoals bij B x D = 1.
Dan kan B slechts 1 zijn en dat geldt ook voor D.
In E – D = 2 is E dan dus 3. In E x F = 12 is F dan 4. In C + E = 6 is C 3. In A + C = 8 is A 5. Een makkelijke opgave dit keer:

A=5 B=1 C=3 D=1 E=3 F=4

0-0-0

[42]
EEN KWESTIE VAN (OP)TELLEN

Je beschikt over de getallen 1 t/m 23

Kies er 12, en zet ze zodanig in de hokjes dat ze opgeteld, zowel horizontaal als verticaal als antwoord 40 hebben.

Elk getal mag maar 1x worden gebruikt.

Oplossing:

Hoewel de opgaven in deze rubriek meestal voor ca. 12-jarigen en ouder zijn, is deze opgave ook geschikt voor vanaf 3e klas; immers, het gaat erom dat je getallen (hier onder de 40) kan splitsen.
Je moet ook durven beginnen, bv. bovenste rij van 4 hokjes (= horizontaal; verticaal heet kolom) met:

willekeurig: 15 10 =(25) Je hebt nu 40 – 25 = 15 over; die moet je splitsen, willekeurig in bv. 14 1
De tweede rij net zo: 2 7 18 13

Je hebt nu:
15 10 14 1
2 7 18 13

De eerste kolom is: 17. Over 23 ; te splitsen, bv. 20 3
De tweede kolom is: 32. Over 8; te splitsen, bv. 6 2, steeds erop lettend dat je geen zelfde getallen gebruikt.


	20	6
15	10	14	1	40
2	7	18	13	40
	3	2
	40	40

Zo zijn er veel oplossingen mogelijk:


	6	7
3	21	14	2	40
8	12	9	11	40
	1	10
	40	40

	21	20
23	13	3	1	40
18	4	8	10	40
	2	9
	40	40

0-0-0

[41]
HET GROOTSTE GETAL MET VIER ENEN

Wat is het grootste getal dat je kunt schrijven met vier enen?

Oplossing:

De klas die machtsverheffen heeft gehad, zou het moeten kunnen vinden:

elf tot de elfde macht: 11¹¹

0-0-0

[40]
MAAK 100 MET 5 DEZELFDE CIJFERS

Laat 4 manieren zien waarop je met 5 dezelfde cijfers een som maakt die als antwoord 100 heeft.

Oplossing:

met enen: 111 – 11 = 100
met drieën 33 x 3 + 3/₃= 100
met vijven: 5 x 5 x 5 – 5 x 5 = 100
of (5 + 5 + 5 + 5) x 5 = 100

0-0-0

[39]
EUROBILJETTEN

Als je in een euroland op vakantie gaat en je wil alle euromunten en -biljetten van dat land als verzameling meenemen, wat kost je dat?

(Er bestaan biljetten van 5, 10, 20, 50, 100, 200 en 500 euro.
Er bestaan munten van 1, 2, 5, 10, 20, 50, 100 en 200 eurocent.}

Oplossing: je betaalt er 888,88 euro voor.

0-0-0

[38-1]
PLAATS DE GETALLEN

Je beschikt over de getallen: 2 5 6 8 9 10

Plaats deze zo op de zwarte stippen die 25 omgeven, dat ze opgeteld 25 zijn; en zo rond 180 dat deze vermenigvuldigd 180 zijn en zo rond 80 dat ze vermenigvuldigd 80 zijn.

Oplossing:

Het is aan te raden met de vermenigvuldigingen te beginnen: die vragen vaste vermenigvuldigers. M.a.w. met welke cijfers kan je 80 maken: 2, 5, 8, 10 en daarvan: met welke 3. Dat kan alleen met 2 x 5 x 8. De 10 kan daar niet bij. Die heb ik wel nodig om 180 te krijgen: 10 x — de 2 andere cijfers kunnen alleen maar 2 en 9 zijn.
Nu valt op dat de 2 een gemeenschappelijke is: die komt dus midden boven. De 6 wordt in de vermenigvuldiging niet gebruikt, dus hoort die bij 25 en wel in de onderste punt. Voor 25 moet ik verder nog 2 cijfers vinden die samen 25 – 8 = 17 vormen. Dat kunnen alleen 8 en 9 zijn. Je weet al bij welk getal die horen: de 9 bij 180 en de 8 bij 80. Nu kun je ook de andere cijfers plaatsen:

0-0-0

[38-2]
PLAATS DE GETALLEN

Je beschikt over de getallen: -7 -3 1 2 10 14

Plaats deze zo op de zwarte stippen dat ze vermenigvuldigd het product 42 zijn en opgeteld: 5 resp. 4.

Oplossing:

Bij vermenigvuldigen horen vaste getallen. Met de positieve getallen krijg je geen 42, dat betekent dat er 2 negatieve getallen nodig zijn, dus – 7 x – 3 = 21, dus nog nodig x 2. Het gaat bij 42 om 4 stippen, het 4e getal rond 42 is dus de 1.

Blijven 14 en 10 over, om daar 5 en 4 van te maken. Daarvoor heb ik zeker -7 nodig, die zet ik bovenaan op de middenstip. Als ik die van 14 aftrek, houd ik 7 over; om 4 te krijgen moet -3 genomen worden. Dus komt 14 bovenaan helemaal rechts, -3 op de stip onder de 4.
Aan de andere kant heb ik de 10 nodig, -7 = 3, daarbij gevoegd de 2 = 5.
De 1 komt dus helemaal beneden:

0-0-0

[38-3]
PLAATS DE GETALLEN

Je beschikt over de getallen: -15 -10 -5 -5 1 4

Plaats de getallen op de zwarte punten zodat ze opgeteld (de som) gelijk zijn aan het getal dat ze omsluiten in de gearceerde velden en vermenigvuldigd (het product) gelijk zijn aan het getal dat ze omsluiten in het witte veld.

Oplossing:

het handigst is de vermenigvuldiging het eerst te onderzoeken: deze heeft immers vastliggende cijfers, hier voor -20 kunnen dat alleen -5, 4 en 1 zijn.
Met 2 ervan en 2 andere moet er dan optellend – 15 uitkomen. -5 kan niet, want met een combinatie van de andere cijfers ontstaat nooit -15, dus -5 komt geheel rechtsboven. Alleen als ik deze 1 en 4 = 5 optel bij – 5 en – 15, krijg ik de gevraagde optelling in het gearceerde vlak: – 15.
Over blijft – 10; deze moet tot – 21 worden. Dat kan alleen met -10 en -15 en 4, wat betekent dat 4 middenboven komt en -10 geheel links. -15 komt dan in de benedenpunt van -21 en blijft -5 over voor de benedenpunt van -15; 1 staat in de benedenpunt van -20:

0-0-0

[38-4]
PLAATS DE GETALLEN

Je beschikt over de getallen: -1 -1 1 2 3 5

Oplossing:

Een vermenigvuldiging is makkelijker te maken: de getallen liggen vast: hier, om 5 te krijgen, kun je die alleen maken met 1 en 5 en nóg een 1, maar aangezien je alleen twee negatieve enen hebt, moet je die gebruiken, zodat het product 5 positief blijft.
Als ik de 5 bij de som 1 laat horen, zijn er negatieve getallen nodig en die zijn er niet meer, dus komt 5 helemaal linksboven en de -1 en -1 op de andere stippen rond product 5.

-1 + -1 = -2. Om som 1 te krijgen moet ik dus 2 getallen vinden die opgeteld bij -2, 1 zijn. Daar kan niet de 3 bij, want dan krijg ik als antwoord 1, terwijl er nóg een getal bij moet. De 3 komt dus helemaal rechtsboven.

Om som 4 te maken, heb ik al -1 + 3 = 2; daar moet dus nog een 2 bij. Dan blijft de benedenpunt over voor de 1. Klaar!

0-0-0

[38-5]
PLAATS DE GETALLEN

Je hebt de beschikking over de getallen: 1 2 3 4 7 8

Plaats de getallen zodanig op de zwarte stippen dat ze opgeteld (de som) gelijk zijn aan het getal in het gearceerde veld dat ze omsluiten en vermenigvuldigd (het product) gelijk zijn aan het getal in de witte velden die ze omsluiten.

Oplossing:

Door eerst naar het product te zoeken, vallen altijd wel een paar cijfers uit omdat die geen deel uit kunnen maken van de vermenigvuldiging, zoals hier bijv. 7 die nooit tot 48 leidt. De 1 kan ook niet, want dan zou er – naast de 8 – nog een 6 moeten zijn en die is er niet; die 6 is er wél in de vorm van 2 x 3; ook met de 4 en twee van de andere cijfers kan geen 48 worden gemaakt. Dus voor 48 gaat het om 2, 3, 8; als je de 2 en de 3 gebruikt om 168 te maken, heb je ook de 4 en de 7 nodig; als we de 2 midden boven zetten, moeten we of met de 7 of met de 4, 13 kunnen maken: 2 + 7 = 9, dan hebben we een 4 nodig voor rechtsboven, maar die komt bij deze combinatie onder in de punt; de combinatie 2 + 4 = 6, vraagt om 7, maar die staat bij déze combinatie onder in de punt: de 2 kan niet boven midden; hoe zit dat met de 3. Dan hebben we 3 + 4 = 7, om 13 te maken hebben we een 6 nodig en die is er niet: ook 3 + 7 kan geen 13 worden (nóg een 3 nodig) dus 3 kan niet midden boven, dan blijft voor die plaats 8 over.
168 moet nu in ieder geval worden gevormd met een 8. Maar ook de 13. Dan kan rechtsboven nooit de 7 zijn en deze wordt dus ook een factor van 168. 7 x 8 = 56; ik heb nog de beschikking over 1, 2, 3 en 4, waarvan ik er twee nodig heb: dat kunnen alleen 1 en 3 zijn: 1 x 3 x 7 x 8 = 168.
De 3 komt dus onder de 48, de 2 staat boven links. De 7 onder in de punt. De 1 komt nu onder de 13 en de 4 rechtsboven.
Nu kloppen de combinaties.

0-0-0

[38-6]
PLAATS DE GETALLEN

Je beschikt over de getallen:

-1 4 6 7 12 14

Plaats de getallen op de zwarte stippen zodat ze opgeteld (de som) gelijk zijn aan het getal in het gearceerde veld en vermenigvuldigd (het product) gelijk zijn aan het getal in het witte veld.

Oplossing:

Omdat je bij het gegeven product (-42) gebonden bent aan factoren, kijken we eerst naar de getallen die -42 kunnen maken. 14 (er is geen 3), 12 en 4 zijn geen factoren, dus blijven -1, 6 en 7 over, die inderdaad vermenigvuldigd -42 zijn.
Waar ze rond de -42 komen te staan is afhankelijk van de andere getallen waarmee we resp. 17 en 32 moeten maken door ze op te tellen.
Kijken we eerst dan maar naar 17. Met 6 of 7 en een van de andere getallen lukt dat niet, dus blijft -1 over die dan het gemeenschappelijke getal van -42 en 17 wordt, dus in het midden op de bovenste lijn komt te staan. De 4 en de 14 en de -1 vormen samen 17. Heeft de 32 nu de 14 of de 4 nodig? 4 valt af, dus die komt boven helemaal rechts en 14 in de onderpunt van 17. De 12 kan dan alleen in de onderpunt van 32.
Voor 32 heb ik nu: 14 en 12 en -1= 25: er is nog 7 nodig, die komt in de onderpunt van -42, de 6 dus helemaal rechts boven. Klaar.

0-0-0

[38-7]
PLAATS DE GETALLEN

Je beschikt over de getallen: -6 2 5 10 11 17

Die moeten op de zwarte stippen komen, zodanig dat het getal dat ze omsluiten, wat -60 betreft, ontstaat door die getallen te vermenigvuldigen; de getallen in de gearceerde velden door op te tellen.

Oplossing:

Een product – het resultaat van een vermenigvuldiging – vind je sneller omdat niet ieder getal in aanmerking komt. Hier dus: 11 en 17. Het resultaat moet negatief zijn: – 60, dus is in ieder geval de -6 nodig en omdat je nog twee getallen nodig hebt, valt ook 10 af en blijven 2 en 5 over die samen met -6 vermenigvuldigd -60 zijn. Een snelle blik leert dat -6 niet meer mee kan doen om de optelling 35 en/of 29 te maken, dus -6 komt bovenaan links.

We hebben nu nog 2, 5, 10, 11, 17 . Alleen de combinatie 2 + 10 + 17 = 29. De 2 hoort dus zowel bij -60 als bij 29, wat betekent dat de 2 boven in het midden komt en dat houdt in dat de 5 in de punt onder de -60 staat.
Om 35 te maken heb je nu al 2 + 5; van de overige getallen heb je nodig 11 + 17, d.w.z. de 10 staat boven rechts. De 17 staat dan in de onderpunt van 29 en de 11 verhuist naar de onderpunt van 35:

0-0-0

[38-8]
PLAATS DE GETALLEN

Je beschikt over de getallen: 1 2 3 3 7 8

Plaats deze op de zwarte stippen. 42 en 6 worden dan omsluiten door 3 getallen, 48 door 4. Als voorbeeld: deze bij de 48 behorende 4 getallen moeten vermenigvuldigd 48 zijn. Zet de gegeven getallen nu zo op de stippen dat ook 6 en 42 het resultaat van een vermenigvuldiging zijn.

Oplossing:

Het zal al snel duidelijk zijn dat de 8 en de 7 niet rond de 6 kunnen; de 8 niet bij 42 kan horen. Dan blijft er maar 1 plaats over: bij 48 onder in de punt. De 7 kan alleen bij de 42 horen, dus bovenaan links. Deze 42 heeft met 7 een 6 nodig, die alleen gevormd kan worden door 2 x 3. Die 6 (2 x 3) heeft ook 48 nodig en aangezien 48 gemaakt moet worden met 4 getallen, kan dat alleen nog met de 1. Die 1 hoort echter ook bij 6. Die kan alleen gemaakt worden door 1 x 2 x 3. Voor die 1 blijft ook maar 1 plaats over: de onderpunt van 6. Zowel 42, 48 en 6 hebben de 2 nodig. Die kan dus alleen op de middenpunt boven. Voor de 2 drieën blijft dan de plaats rechtsboven en in de onderpunt van 42

0-0-0

[38-9]
PLAATS DE GETALLEN

Gegeven de getallen: -7 -3 2 9 14 21

Plaats deze zodanig op de zwarte punten dat ze, rondom 34, opgeteld ook 34 zijn; dit zelfde geldt voor 20 en dat ze vermenigvuldigd rondom 42 geplaatst, ook als antwoord 42 zijn.

Oplossing:

Omdat je een vermenigvuldiging hebt, is het slimmer daarmee te beginnen. Het product eist een aantal getallen voor zich op of sluit andere uit, zoals bijv. hier de 9 die geen 42 kan worden.
21 en 14 kunnen wél 42 worden, met resp. de 2 en de 3, maar aangezien het om 3 getallen gaat, moet je een 1 hebben en die is er niet. Dus blijven -7, -3 en 2 over: die zijn vermenigvuldigd: 42.
Als ik -7 en -3 optellers van 34 laat zijn, moeten de 2 andere getallen samen 44 zijn, maar die zijn er niet; hetzelfde geldt ook voor -7 en 2: je kan ook niet aan (-7 +2 +34) = 39 komen, dus -7 kan niet bij 34 horen en komt dus op de punt linksboven.
Om 34 te kunnen maken hebben we nu dus: -3 en 2 = -1. Dan moeten we 2 getallen hebben die samen 35 zijn. Die hebben we met 14 en 21. We hebben ook de 9 nog, die nu blijkt alleen op de rechterpunt boven te kunnen staan. Dan zie je dat 21 niet bij 20 kan horen, want 21 + 9 = 30 en je hebt hooguit -3 en geen -10 om die 20 te vormen. Nu weet je dat 21 in de onderpunt komt. De 14 komt dan op de punt 0nder de 20.Je hebt nu 14 en 9 = 23. Om daar 20 van te maken moet -3 ingeschakeld worden. Die komt dus in het midden op de bovenlijn. Dan blijft -2 over voor de overgebleven punt. Opgelost!

0-0-0

[38-10]
PLAATS DE GETALLEN

Je beschikt over de getallen:

-4 -1 2 4 5 7

Plaats de getallen op de zwarte stippen zodanig dat ze vermenigvuldigd (het product) gelijk zijn aan het getal in het veld dat ze omsluiten.

Oplossing:

Het is al snel duidelijk dat bijv. de 5 een gemeenschappelijke factor is van 20 en -140 en dus niet rond de -14 kan staan; dat geldt ook voor -4 en +4. De factoren die -14 moeten opleveren zijn dus: 2; 7; en -1. De 2 wordt dan ‘verbannen’ naar helemaal rechtsboven; de 7 kan geen factor zijn van 20, dus deze komt onder de 14 te staan; blijft -1 over voor de bovenste lijn in het midden. De 5 is nodig om 20 te maken, maar ook voor de -140, dus de 5 staat onder de 20. Om 20 te krijgen heb je nu: -1 en 5, dus daar moet nog een negatief getal naartoe: -4, die komt dus helemaal links te staan. Blijft + 4 over voor de onderste plaats. Alles klopt. Opgelost!

0-0-0

[38-11]
PLAATS DE GETALLEN

Je beschikt over de getallen:

-13 -4 -2 6 7 11

Plaats de getallen op de zwarte stippen zodat ze opgeteld (de som) gelijk zijn aan het getal in het gearceerde veld en vermenigvuldigd (het product) gelijk zijn aan het getal in het witte veld.

Oplossing:

Een product vind je makkelijker dan een optelling. 11 bijv. kan nooit 56 worden, 6 ook niet, maar ook 13 niet. Blijven voor 56 -4, -2, en 7 over: -4 x -2= +8 x 7 = 56
-4 en -2 en 7 komen dus rondom de 56 te staan, maar waar?.
Twee van deze drie getallen moeten als optellers, met nog twee andere, leiden tot -8

Stel je kiest -2 en 7. Dat is opgeteld 5. Je moet echter naar -8; dan zou -13 kunnen, maar het gaat om 4 getallen en nog één erbij, leidt niet meer tot -8. Dat geldt ook voor de combinatie 7 en -4. Dat is 3. Om bij -8 te komen moet je dus twee getallen hebben die samen -11 zijn en die heb je niet. Dus 7 kan niet het getal zijn om -8 te krijgen. Dus komt de 7 helemaal links boven.

Nu moeten we -8 krijgen door -2 en -4, dat is -6. Twee getallen moeten nu samen -2 vormen uit de overgebleven getallen. Dat kunnen alleen -13 en 11 zijn.

Dat betekent dat 6 helemaal rechtsboven staat. Deze 6 moet met twee getallen samen 13 vormen; die twee getallen moeten dus samen 7 zijn. In aanmerking komen combinaties van -2; -4; 11 en 13. Daaruit volgt dat het om -4 en 11 gaat. -4 was echter ook nodig om 56 te maken, dus die staat midden op de bovenlijn; dan moet de 11 in de benedenpunt van veld 13. De onderste punt blijft over voor -13, daar -2 bij 56 hoort.

0-0-0

[38-12]
PLAATS DE GETALLEN

Gegeven de getallen: 1 2 2 3 4 5

Plaats deze zodanig op de zwarte punten dat ze, vermenigvuldigd, het antwoord zijn van het gegeven getal dat ze omsluiten: 10 16 12

Oplossing:

Voor een 5e-klasser moet zo’n opgave te doen zijn.
Vooraf kunnen er al wat zekerheden worden ingebouwd: de 5 kan niet bij de 12 en de 16 horen, dus wel bij de 10: geheel links boven.
De 3 kan niet bij de 10 en de 16 horen, dus bij de 12: in de onderste punt.

Dan volgt de rest eigenlijk vanzelf:
De 12 kan geen 4 meer krijgen, dus is deze voor de 16: geheel rechts boven.
Om 16 te kunnen krijgen, moet de 4 nog vermenigvuldigd worden met 2 x 2: die behoren dus bij de 16.
De 1 blijft over: op de onderpunt van de 10:

0-0-0

[38-13]
PLAATS DE GETALLEN

Met negatieve getallen (vanaf eind klas 7, klas 8:

Je beschikt over de getallen:

-1 -1 1 2 3 5

Plaats de getallen op de zwarte stippen zodat ze opgeteld (de som) gelijk zijn aan het getal in het gearceerde veld en vermenigvuldigd (het product) gelijk zijn aan het getal in het witte veld.

Oplossing:

Omdat de 5 door vermenigvuldigen moet ontstaan, heb je niets aan de getallen 2 en 3. Blijven over; -1 -1 en 1 (Na de behandeling van de negatieve getallen, zou de leerling onmiddellijk moeten zien dat 1 niet kan, want je moet dan ook -1 gebruiken en dan wordt 5 negatief. Dus -1 x -1 x 5 zijn de getallen van de linker driehoek. Als je de 5 op de zijde van de ruit zet, kan door optelling nooit meer een 1 komen (het antwoord van de ruit), dus staat de 5 helemaal
linksboven.
Die 1 wordt opgebouwd uit -1 + -1 = -2. De 3 kan niet, want dan hebben we al 1, terwijl er nog een zwarte stip bezet moet worden. Dan kan alleen de 2 en de + 1; de 3 komt dus helemaal rechtsboven. De 4 wordt nu opgebouwd uit: -1 + 3 = 2, daar moet dan een 2 bij. De 1 komt dan onder in de punt.

0-0-0

[38-14]
PLAATS DE GETALLEN

Plaats de getallen in de open cirkels zo dat ze opgeteld (de som) gelijk zijn aan het getal dat ze omsluiten in de grijze velden en vermenigvuldigd (het product) gelijk zijn aan het getal dat ze omsluiten in het witte veld.

Oplossing:

De vermenigvuldiging vind je het makkelijkst: het product – 60, kan alleen gemaakt worden met -6 x 2 x 5
29 kan alleen de som zijn van 2 + 10 + 17; dat betekent dat -60 en 29 de 2 gemeenschappelijk hebben: die komt dus middenboven.
Om 35 te krijgen heb je zeker de 17 nodig, om 29 ook, dus die komt op de gemeenschappelijke plaats: in de punt onder 29.
Dan komt de 10 rechtsboven
De 11 kan dan niet anders dan in de onderpunt van 35 komen.
Voor 35 heb je al: 2 + 17 + 11 = 30, waaruit volgt dat de 5 in de onderpunt van – 50 komt.
Dan blijft voor -6 alleen de positie bovenaan links over.

0-0–0

[38-15]
PLAATS DE GETALLEN

Je beschikt over de getallen -9 -8 -6 -2 7 9

Plaats deze zo op de zwarte stippen dat ze, vermenigvuldigd, als uitkomst hebben, het getal waar ze rondomheen staan.

Oplossing:

Door even te kijken en te proberen, vind je al snel dat 112 is bijv. 2 x 7 x 8; de 6 en de 9 kunnen daar niet.
De -6 is ook geen deler van 567, dus blijft er maar één plaats over: in de benedenpunt van 756.
Als de leerlingen al bekend zijn met de negatieve getallen, weten ze nu dat er – omdat 756 positief is, nóg een negatief cijfer bij moet: 756: 6 = 126 en die heeft alleen de 9 als deler: 126 : 9 = 14. Deze 14 bestaan dan weer uit 2 x 7
Hieruit volgt al, dat 112 en 756 de -2 gemeenschappelijk hebben en omdat 567 geen 2als deler heeft, komt deze -2 in de onderpunt van 112.
Nu blijken 112 en 756 de 7 gemeenschappelijk te hebben: die komt dus in het midden boven. De 8 komt dan dus rechtsboven.
Omdat 756 nog een negatief getal nodig heeft, kan dat niet anders dan -9 zijn, die in de onderopunt van -567 komt te staan; de 9 kan dan alleen nog linksboven. Bij controle klopt het:

0-0-0

[37]
HOEVEEL REPEN?

Een chocoladereep kost € 2,50.
Op iedere reep zit een zegel. Als je vier zegels inlevert krijg je gratis zo’n zelfde chocoladereep.
Hoeveel repen krijg je – als je dat wil – voor € 25,–

Oplossing:

Voor € 25,– koop je 10 repen – je hebt dus 10 zegels. Als je wil kun je voor 8 zegels nog 2 repen krijgen. Je houdt 2 zegels over, maar die 2 repen hebben ook nog 2 zegels, dus heb je er 4 voor nog een reep. Totaal 13.

0-0-0

[36]
HOE OUD

Iemand die graag in raadsels spreekt, antwoordde, gevraagd naar zijn leeftijd:

Neem mijn leeftijd over 3 jaar, vermenigvuldig die met 3, je hebt een eerste getal.
Neem dan mijn leeftijd van 3 jaar geleden en vermenigvuldig die met 3, je hebt een tweede getal.
Trek het tweede van het eerste af en je weet hoe oud ik ben.

Oplossing: je kunt altijd met proberen beginnen, met een willekeurig getal.
Als je deze opgave tegelijk door veel kinderen laat maken die allemaal een verschillend uitgangsgetal nemen, komt er bij ieder hetzelfde antwoord uit.

Stel: de vraagsteller is 25. 3 erbij 28, keer 3: 84
25, 3 eraf 22, keer 3: 66. 84 – 66 = 18 of

stel de leeftijd op 68, 3 erbij 71, keer 3: 213
68, 3 eraf 65 x 3: 195. 213 – 195 = 18

Enzovoort.

Met algebra:

(X + 3) 3 — (X – 3)3 = X
(3X + 9) — (3X – 9) = X
X = 18

Als je de hele klas hebt laten kiezen, is het niet moeilijk (nog eens) te laten zien, dat X staat voor ieder getal dat elke leerling heeft gekozen; dat je met algebra dus ‘in één keer klaar bent’ (tijdwinst, o.a.)

0-0-0

[35]
HOE ZIT DAT?

Nadat je twee sommen hebt uitgerekend kun je de rest meteen op papier zetten. Hoe zit dat?

987654321 x 9 = …….. 89

987654321 x 18 =

987654321 x 27 =

987654321 x 36 =

987654321 x 45 =

987654321 x 54 =

987654321 x 63 =

987654321 x 72 =

987654321 x 81 =

Oplossing:

Het product van de eerste vermenigvuldiging is: 8888888889; van de tweede:
17777777778

Het getal 9 heeft ons al meer interessante verrassingen gezorgd!

Dat de tafelrijgetallen nu ook nog eens vermenigvuldigd moeten worden met 987654321 is al heel bijzonder.

Het uitrekenen is een uitstekende mogelijkheid het vermenigvuldigen nog eens grondig te herhalen – met de tafels natuurlijk!

En een mooie aanleiding voor waarnemen: vergelijk de twee antwoorden. Wat zie je?
Bijv. de laatste 9 is een 8 geworden; de achten zijn zevens geworden, vooraan is er een 1 bijgekomen.

Zou je nu het derde antwoord kunnen voorspellen?
Het eindigt wellicht op 7 en ervoor -goed tellen – komen dan 9! zessen met een 1

26666666667. Dat moet natuurlijk gecontroleerd worden: vermenigvuldigend, maar ook kan het gemak van ‘vermenigvuldigen is herhaald optellen’nu zijn dienst bewijzen. Maar…hoe zat het ook al weer met ‘getallen precies onder elkaar?’

Immers: 17777777778
8888888889 +
———————–
is inderdaad 26666666667

Vermenigvuldigen is hier lastiger dan optellen.

Nu zijn de antwoorden snel gevonden:

35555555556; 44444444445.
Misschien is het nu tijd om het getal voor de leesbaarheid te schrijven met de punten:
44.444.444.445 en goed uit te spreken. Dat vergemakkelijkt meteen weer de ‘voorspelling’: 53.333.333.334; 62.222.222.223; 71.111.111.112; 80.000.000.001 en ten slotte: je zou willen voorspellen: 89.999……….., maar het is: 88. 888.888.890 (10 x het getal waarmee we steeds herhaald hebben opgeteld!)
Waaruit we de wijze les kunnen trekken dat voorspellen toch altijd gevolgd moet worden door controle!

0-0-0

[34]
REKENKRUIS’WOORD’

horizontaal verticaal

a) 43 x 35 a) het produkt van 977 en 16

d) (44 x 25) – (35 x 25) b) 24 x 43 – 25 x 18

g) 4 x 89 min het dubbele van 149 c) getal, dat geschreven kan worden als 33 x 181

h) 2 x (5 x 3 x 6 x 5 – 3) d) het dubbele van 2 x 8 x 9

1) 7 x 11 x 9 x 9 e) 12 maal 247

k) het product van 31 en 28 f) 33 x 27 – 7 x 7 x 7

l) 15 x 18 plus het dubbele van 83 j) het product van 69 en 5

n) getal dat geschreven kan worden als m) 14 x 27 + 4 x 8 x 10 + 1
5 x 57
o) 14 maal 601
q) 26 x 104 + 56 x 19 – 500
p) 25 maal 31 min 31 x 22 r) product van 349 en 21

s) 15 x 17 + 3 x 79 s) 22 x 13 – 3 x 3 x 3 x 3 x 3

t) 7 x 309 t) 8 x 34 – 13 x 19

v) getal dat geschreven kan u) 5 x 47 ~ 2 x 83
worden als het product van 8 en 79 w) 21 x 36 – 4 x 181

x) 24 maal 24 min 3 x 3 x 3

y) 11 x 439

0-0-0

[33]
DE APENROTS

Op een rots in een beroemde dierentuin zit een onbekend aantal krulstaartapen. Als er nu nog eens eenmaal, een halfmaal en een kwartmaal zoveel krulstaartapen komen aangeslingerd en ten slotte nog 1 oude krulstaartaap, dan krioelen er precies 100 apen op die rots.

Hoeveel krulstaartapen zaten er eerst op die rots?

Oplossing:

Je kunt schatten: 40 is te veel; 30 te weinig. Ergens tussen 30 en 40; een getal dat door 2 en 4 deelbaar is: 32 of 36. Uitproberen: 36.

Met algebra: 100 – 1 = X + X + ½X + ¼X = 2¾X 2¾X=99 X=36

0-0-0

[32]
VEELVOUD VAN 7

Welk veelvoud van 7 kun je delen door 2, 3, 4 en 6, waarbij je er steeds 1 overhoudt?

En wat is dat veelvoud van 7 als ook de 5 meedoet?

Leerlingen vanaf klas 5, zeker 6 en 7 moeten in staat zijn deze vraag te beantwoorden.
De tafels moet je wel goed kennen.
Welke getallen hebben 2, 3, 4 en 6 allemaal in hun tafelrij.
12 (veelvoud zeven: 14) gaat niet op; 24 (28 gaat niet op); 36 (gaat niet op); 48:
(veelvoud 49) gevonden!

Je kunt verder zoeken of er nog meer mogelijkheden zijn.

Wanneer de 5 erbij komt, zou je zo kunnen (moeten) redeneren: het kan geen even getal zijn, want dan blijft er bij 2 en/of 4 en 6 nooit 1 over; wanneer het op 3, 7 of 9 eindigt, blijft er, gedeeld door 5 altijd meer over dan 1; dus moet het getal wel op 1 eindigen.

Nu dus de 7-vouden zoeken die eindigen op 1: dan moet 7 steeds worden vermenigvuldigd met een getal dat op 3 eindigt: keer 3: 21-nee: deelbaar door 3; keer 13: 91? gedeeld door 4, nee 3 over; x 23: 161? gedeeld door 3? nee, 2 over; x 33: 231 dan? gedeeld door 4, nee 3 over; x 43: 301: bingo!

0-0-0

[31]
SIGAARTJE?

1 sigaar weegt 3 gram en een halve sigaar.

Hoeveel weegt anderhalve sigaar?

oplossing:
Als er sprake is van een halve sigaar, dan is er nog een helft. Die helft weegt hier 3 gram. De hele sigaar weegt dus 6 gram en anderhalve dan 9 gr.

0-0-0

[30]
EEN JUWEELTJE

Toen een Indiase prinses jaren geleden een kostbare steen kreeg, vond ze hem zo mooi dat ze een kunstenaar opdracht gaf deze te tekenen. Toen ze de tekening zag, ontdekte ze hoeveel driehoeken erin verborgen waren. Ziet u het ook?

Oplossing:

72.

0-0-0

[29]
HET WONDERPLANTJE

Een Chinees mandarijn plantte in zijn tuinvijver een wonderplantje, dat zich iedere dag verdubbelde. Zijn tuinvijver was na 30 dagen helemaal gevuld. De mandarijn keek vergenoegd naar het resultaat maar vroeg zich tóch af hoelang het geduurd zou hebben als hij met 4 wonderplantjes was begonnen in plaats van 1.

Ja, hoe lang?

Oplossing:

Na de 1e dag heeft het plantje zich verdubbeld: er zijn er 2.
Na de 2e dag hebben deze plantjes zich verdubbeld: er zijn er 4.

Als de mandarijn met vier plantjes zou zijn begonnen, is het alsof hij 2 dagen later begint dan met 1 plantje. Het duurt bij 4 plantjes dus geen 30 dagen, maar 2 dagen minder: 28 dagen.

0-0-0

[28]
HOEVEEL KOST ELK?

Een fles en een kurk kosten samen € 1,10. De fles is precies € 1 duurder dan de kurk. Hoeveel kost de fles; hoeveel kost de kurk.

Je kunt simpelweg redeneren: als de fles € 1 kost, kost de kurk € 0,10; dan is het verschil € 0, 90. Het moet echter € 1 zijn. Je komt dus € 0,10 te kort. Wanneer je dit tekort over fles en kurk verdeelt, moet de een er € 0,10 : 2 = € o,o5 bijkrijgen: de fles kost dus € 1,05 en de kurk € 0,05

Met algebra en de kennis van het optellen van negatieve getallen kan het ook:

F + K = 110
F – K = 100
————+
2F = 210 → F = 105 → K = 5

0-0-0

[27]
WELKE KLOK GEEFT DE JUISTE TIJD AAN?

In een kamer staan twee klokken: een oude Regulatorklok die 5 minuten per dag achterloopt en een kostbare staande klok uit 1898 die al maanden stilstaat.

Welke van beide klokken geeft, gerekend over een heel jaar, de meeste keren de juiste tijd?

De stilstaande klok geeft 2x per etmaal de juiste tijd aan. Uitgaande van 365 dagen betekent dit dat hij 730 keer de juiste tijd aangeeft.

De achterlopende klok geeft op de dag waarop de vergelijking start, laten we aannemen om 12u, de juiste tijd. In dat etmaal dus maar 1 x, want hij begint dan ook met achterlopen. Dit t.o.v. de andere klok laat al zien welke het vaakst de juiste tijd aangeeft: de klok die stilstaat.

Als je nog wil weten hoe vaak de achterlopende klok de juiste tijd aangeeft in dat jaar, weet je dat hij na 12 dagen van 5 min = 1 uur achterloopt. Pas na 11 x 12 dagen loopt hij weer even gelijk, dus na 132 dagen. En na 132 dagen weer. Nog eens 132 dagen zitten niet meer in dat jaar. Dus in dat jaar geeft hij maar, vanaf de start, 3 keer de juiste tijd aan.

0-0-0

[26]
WAT KOMT OP DE PLAATS VAN HET VRAAGTEKEN

14 ? 9

30 28 13

48 39 15

Oplossing:

Kun je een soort wetmatigheid ontdekken, bijv.

Het rechter getal van het linker afgetrokken geeft als antwoord een getal dat de helft is van het linker, of het linker is 2 x dat getal.

28 – 13 = 15 30 = 2 x 15
39 – 15 = 24 48 = 2 x 24

14 moet dus 2 x een getal zijn: dat getal is dan 7

Deze 7 moet het resultaat zijn van een aftrekking met 9: dat is het getal 16.

0-0-0

[25]
KUN JE DIT OPTELLEN

Oplossing:

Hier staan de getallen 1 t/m 9 – steeds gespiegeld tegen elkaar.

Het gaat dus om de getallen 11, 22, 33 enz. t/m 99.

De optelling daarvan is 495

0-0-0

[24]
PLAATS DE GETALLEN

Plaats in de lege cirkels de getallen die ontbreken. Je kunt kiezen uit de getallen 1 t/m 16. Elk getal mag maar eenmaal worden gebruikt. De optelling van de zes lijnen moet steeds 34 zijn:

rekenraadsel 14

Oplossing:

Hoe dichter je bij de 34 komt, des te minder getallen komen in aanmerking.

15 + 14 komen er het dichts bij. Te verdelen 5. Dat kan in 2 + 3 en 1 + 4. Er staat al een 3, dus blijft 1 + 4 over.

Kies je in 16 + 11 voor de 4, heb je nog een 4 nodig – dat mag niet; de lijn wordt dus 16 + 1 + 6 + 11 of 6 + 1

De lijn 15 + 6 + 14 komt al boven 34, dus daar kan de 6 niet; die lijn wordt dus:
16 + 1 + 6 + 11

De andere lijnen kunnen dan makkelijk worden gevonden:

15 + 1 + 4 14;
16 + 4 + 9 + 5;
14 + 9 + 8 + 3;
5 + 8 + 10 + 15;
15 + 6 + 10 + 3

0-0-0

[23-5]
Rekenpuzzel

Vul het diagram zo in dat de cijfers 1 t/m 8 2 x voorkomen en dat de uitkomst van de horizontale, verticale en de 2 twee lange diagonale hokjes het totaal vormen dat in de gekleurde hokjes staat aangegeven.

Oplossing:

Rij 1: som = 12; er moeten er 6 bij. Dat kan niet met 3 + 3 (er zijn al twee drieën), wat ook geldt voor 5 (+ 1).
Blijft over: 2 + 4

Dan proberen: 1e rij: 5 7 2 4

Dan 3e kolom: 2 + 5 + 8 + 3: dat gaat nog steeds

Dan diagonaal van linksboven naar rechtsonder: 5 + 4 + 8 + 1,

dan 4e kolom: 4 + 7 + 6 + 1

dan 2e rij: 2 + 4 + 5 + 7

3e rij: 3 + 1 + 8 + 6. dus 2e kolom: 7 + 4 + 1 + 6

dan 4e rij: 8 + 6 + 3 + 1 en bijgevolg de diagonaal van rechtsboven naar linksonder: 4 5 1 8 en de 1e kolom 5 2 3 8

Hiermee is aan de opdracht voldaan.

Uiteraard kunnen verschillende oplossingswegen worden bewandeld.

0-0-0

[23-4 ]

Oplossing:

Rij 1 en 2 zijn eigenlijk gelijk. De som is 15, terwijl die 18 moet zijn. Over de 2 lege hokjes moet dus 3 worden verdeeld; dat kan alleen met 1 en 2.

Wanneer we ze ‘gewoon’ invullen, wordt de 1e kolom: 8 + 1 + 5 + 4

De diagonaal van rechtsboven naar links beneden wordt dan: 2 + 8 + 4 + 4; maar dat kan niet omdat er dan 3 vieren mee gaan doen, wat niet mag. Dus keren we op de bovenste rij 1 + 2 om in 2 +1. Maar dan krijgen de 3e rij en de 3e kolom een 5 en daarvan zijn er dan meer dan 2, wat niet mag.

Dus draaien we ook in de 2e rij 1 + 2 om.
De 1e kolom wordt dan: 8 + 2 + 5 + 3
In de diagonaal staat dan: 1 + 8 + 6 + 3 = 18

Met deze 6 wordt de 2e kolom: 7 + 1 + 6 + 4= 18
De 3e kolom wordt dan: 2 + 8 + 3 + 5= 18

De 3e rij wordt dan: 5 + 6 + 3 + 4= 18

De 4e rij: 3 + 4 + 5 + 6=18

De diagonaal van linksboven naar rechtsbeneden klopt dan ook en we hebben de cijfers 1 t/m 8 2x, conform de opdracht.

0-0-0

[23-3 ]

Oplossing:

je kunt meteen vaststellen dat 1, 3, 4 niet meer meedoen.

de bovenste rij heeft 11; er ontbreken 7;

deze 7 kan niet bestaan uit 1 + 6; en 3 + 4; dan blijft alleen over 2 + 5;

verder: 2e kolom van links: er ontbreken 9:

deze 9 kan niet zijn 1 + 8; 3 + 6 en 4 + 5; dan blijft 2 + 7 over

verder: in de 3e rij moet samen 13 gevonden worden met 2 of 7: dan kan alleen 7 zijn: de 3e rij bestaat dus uit: 4 7 en 1: het andere getal is dus 6:

3e rij: 4 7 6 1

2e kolom van links is dan: 8 1 7 2

diagonaal van linksboven naar rechtsbeneden: 3 1 6 8

4e rij dan: 5 2 3 8

1e kolom van links dan: 3 6 4 5

diagonaal van linksonder naar rechtsboven dan: 5 7 4 2

1e rij dan: 3 8 2 5

4e kolom: 2 7 1 8

1e rij dan: 3 8 5 2

0-0-0

[23-2]

Oplossing:

de 1e rij biedt nog geen oplossing: de 2 open plaatsen zijn samen 10 (18-8) en deze 10 kan bestaan in 2 + 8 en 5 + 5

de 2e rij: 2 plaatsen voor 11 (18 – 7) : 11 = 2 + 9, maar die 9 doet niet mee; 3 + 8: er zijn al 2 3-en; idem voor 4, dus blijft 5 + 6 over; dit geldt ook voor de 3e rij

wanneer ik in de 3e rij de 6 in de 3e kolom plaats, komt er in de bovenste rij naast de 1, ook een 1; dit betekent dat het dan nog ontbrekende cijfer in de bovenste rij 9 moet zijn, maar die doet niet mee, dus:

3e rij: 4 6 5 3

2e kolom: 1 4 6 7

3e kolom: 2 3 5 8

1e rij: 7 1 2 8

diagonaal rechtsboven-linksbeneden: 8 3 6 1

1e kolom: 7 6 4 1

2e rij: 6 4 3 5

4e kolom: 1 7 8 2

0-0-0

[23-1]

Oplossing:

1e rij: de twee lege hokjes zijn samen 18 – 6 = 12
12 kan zijn: 6 + 6; 7 + 5; 8 + 4 7 + 5 valt af: er zijn al 2 vijven.
Proberen we 6 + 6. Dan heeft de 4e kolom: 6 + 5 + 2 = 13. Om 18 te krijgen moet er 5 bij, maar dat kan niet meer.
Blijven de 8 en de 4. Proberen we de 4. De laatste kolom heeft dan: 4 + 5 + 2 = 11; in het laatste hokje van de 4e kolom komt dan een 7. Dat is een mogelijkheid.
Proberen we de 8. De laatste kolom heeft dan: 8 + 5 + 2 = 15; in het laatste hokje van de 4e kolom moet dan een 3 komen, maar dat kan niet: er zijn er al 2; dus de 1e rij is:

1e rij: 1 5 8 4

4e kolom: 4 5 2 7

dan: 4e rij: 6 2 3 7

dan 1e kolom: 1 8 3 6

nu moet je nog een 1, 4, 6, 7 kwijt

In de 2e rij kan geen 7, want dan kom je boven de 18; die 7 moet dus in de 3e rij komen

Hij kan niet in de 3e kolom, want dan kom je ook boven de 18; de 7 komt dus in de 3e rij en de 2e kolom; dan:

3e rij: 3 7 6 2

dan 2e kolom: 5 4 7 2

dan 2e rij: 8 4 1 5

de diagonalen kloppen zo ook: klaar!

rekenraadsel 11a

0-0-0

[22]
Wat komt op de plaats van het vraagteken?

Vanaf klas 3, 4 moet deze opgave te doen zijn

rekenraadsel 9

Oplossing:

3 gelijke plompenbladeren samen 30:

1 blad = 10

+ 2 gelijke paarden = 18: 2 gelijke paarden 8:

1 paard = 4

4 – 2 klompen = 2: 2 klompen = 2:

1 klomp = 1

Som:

20 + 1 + 4 = 25

0-0-0

[21]
Vul in:

Geen gemakkelijke opgave.
In klas 7 en hoger zou het moeten gaan lukken.

Uitrekenen en invullen. Let goed op de scheidingsstreepjes !

rekenraadsel 5

HORIZONTAAL

51 X 47 + 150
6 X 710 + 2
143 X 129 + 76092
2³ X 9521
4X (6³ + 8⁴) – 2654
181² – 228
73 X 51 + 1751
(186 + 149) X (98 + 183) + 401
345 X 5²
2³X 3³X 251
(2⁶– 2) + 71 111
3 X (5124 + 6499)
5³ X (450 – 1)
20 X 70 – 43
2²X 3 X 17²

VERTICAAL

87 X 239 + 16744
25² + 6
2 X 3 X 1421
(47 + 112) X (312-129) -1504
16³ X 4 + 30
78 X 98 + 478
(983 – 718) X (38 + 225) + 1842
242² + 359
15⁴ + 13018
2²X 3 X (2147 + 3230)
3 X 38 X 40 -9
2⁴ X 2477
345 X 52 + 1
575 X 85 + 62
79 X 83- 135
5 X 113

OPlossing:

51 X 47 + 150=2547 (RIJ 15)
6 X 710 + 2=4262 (RIJ 14)
143 X 129 + 76092=94539 (RIJ 13)
2³ X 9521=76168 (RIJ 12)
4X (6³ + 8⁴) – 2654)=14594 (RIJ 11)
181² – 228=32533 (RIJ 10)
73 X 51 + 1751=5471 (RIJ 9)
(186 + 149) X (98 + 183) + 401=94536 (RIJ 8)
345 X 5²=8625 (RIJ 7)
2³X 3³X 251=54216 (RIJ 6)
(2⁶– 2) + 71 111=71173 (RIJ 5)
3 X (5124 + 6499)=34869 (RIJ 4)
5³ X (450 – 1)=56125 (RIJ 3)
20 X 70 – 43=1357 (RIJ 2)
2²X 3 X 17² =3468 (RIJ 1)

VERTIKAAL

87 X 239 + 16744=37537 (KOLOM 1)
25² + 6=631 (KOLOM 3)
2 X 3 X 1421=8526 (KOLOM 4)
(47 + 112) X (312-129) -1504=27593 (KOLOM 5)
16³ X 4 + 30=16414 (KOLOM 2)
78 X 98 + 478=8122 (KOLOM 3)
(983 – 718) X (38 + 225) + 1842=71537 (KOLOM 4)
242² + 359=58923 (KOLOM 1)
15⁴ + 13018=63643 (KOLOM 5)
2²X 3 X (2147 + 3230)=64524 (KOLOM 2)
3 X 38 X 40 -9=4551 (KOLOM 3)
2⁴ X 2477=39632 (KOLOM 4)
345 X 52 + 1=17941 (KOLOM 1)
575 X 85 + 62=48937 (KOLOM 5)
79 X 83- 135=6422 (KOLOM 2)
5 X 113=565 (KOLOM 3)

rekenraadsel 6

0-0-0

[20]
Zoek het getalwoord onder de pijl

Vul alle 21 woorden in.

Eén woord is al ingevuld.

Daaraan kun je zien hoe het moet.

Als alle woorden goed zijn, krijg je een nieuw woord. Dat woord kun je lezen van boven naar beneden.

Het begint bij de pijl.

Het dubbele van 9.
Zoveel eurocent is een euro waard.
Zeg de tafel van 3 op: 3, 6, 9, 12, enz. Tot 30. Eén van deze getallen moet je hier invullen.
Hoeveel is het verschil tussen 6215 en 6218?
Een getal onder de 60. Je kunt het getal delen door 7.
Een getal tussen 20 en 50.
Sommige maanden hebben zoveel dagen.
Als ze zo oud zijn houden de meeste mensen op met werken.
Aantal vingers aan twee handen
Zoveel dagen heeft een week.
Dit noemen ze wel eens het gekkengetal.
Een héél klein getal,
Het verschil tussen 2639 en 2643.
Wat betekent de 1 in het getal 1975?
Twee keer 35.
Zoveel oren heb je.
De helft van het getal dat je bij nummer 16 opgeschreven hebt
Dit getal noemen ze wel eens het ongeluksgetal.
Een getal tussen 1 en 20
Dit getal onder de 30 kun je delen door 5 en door 4.
De helft van 100.

Oplossing

Oplossing:

Honderdzevenenveertig

0-0-0

[19]
Wat is de waarde van de letters

Maak deze som en zoek uit welke cijfers er op de plaats van de letters moeten staan:

A B
2 C X
A 4 3
5 D 0
B 8 E

Oplossing:

C x B moet op 3 eindigen: dat kan alleen met 1 x 3 of 3 x 1 en 7 x 9 of 9 x 7.

1 en 3 vallen af, immers: dan zou er geen cijfer kunnen staan voor A in A43.

Dus C is 7 of 9 en de 3 komt van 63.

D opgeteld bij 4 = 8. Dat betekent dat D =4

D= ook 2 x B, dus B die 7 of 9 is, moet 2x genomen, als eindcijfer een 4 hebben. Dat kan alleen 7 zijn. B=7 en C=9

Het eindantwoord is dus: 7 8 3. Daaruit lees je af dat A =2.

2 7
2 9 x
2 4 3
5 4 0
7 8 3

0-0-0

[18]
Wat is de som van de getallen 1 t/m 100

Ik kwam bv. deze tegen:

Een trap telt 100 treden. Op de eerste trede staat een duif; op de tweede 2 en op de derde 3, enz. op elke tree 1 meer, tot de honderdste.

Hoeveel duiven zijn dat in totaal.

Oplossing:

Alcuinus lost dit vraagstuk op dezelfde manier op als Gauss, die als kleine jongen op school alle hele getallen van 1 tot en met 100 razendsnel bij elkaar wist op te tellen. Alcuinus legt uit: ‘Neem degene die op de eerste trede zit, en voeg deze bij de 99 die op de 99ste trede zitten, en dat is bij elkaar 100. Zo ook de tweede en de 98ste, en kom wederom op 100 uit. Zo zal er voor elke trede….steeds bij elkaar 100 gevonden worden. De vijftigste trede staat op zichzelf, omdat hij geen partner heeft, en de honderdste is evenzo alleen. Tel alles bij elkaar op en krijg 5050.

De vraagstelling van de som sluit uit dat er op de 100ste trede ook duiven zitten (wat in het antwoord terugkomt, maar wordt toch meegeteld bij het eindantwoord, dat volgens mij dus 4950 had moeten zijn.

Ik heb de opgave dan ook aan de kinderen gesteld mét de 100 erbij. Dan krijg je 50 paren van 101: 5050.
Ik had het voorbereid met het optellen van de getallen 1 t/m 10. Dat zijn 5 paren van 11, dus 55.

Kinderen kunnen dan de smaak te pakken krijgen en zullen ontdekken dat het steeds om de paren gaat en dat je de helft moet nemen van het laatste getal in de opgave:

Tel op: 1 t/m 26 = 26:2 = 13 paren van 1 + 26 = 27.

13 x 27 = 10 x = 270 + 3x = 81 = 351.

Is het getal oneven: t/m 27, dan neem je 26: =351, waarbij de 27 dan nog moet worden opgeteld: 378

Maar ook 1 t/m 100.000 is in no time gedaan:

50.000 x 100.001 = 50.000 x 100.000 = 5.000.000.000 + 50.000 =

5.000.050.000 (uitspraak!)

Stel nu eens dat je alle getallen onder elkaar zou moeten opschrijven. Als je klokt hoe lang je erover doet om 1 t/m 10 onder elkaar te zetten en 99.990 t/m 100.000, blijkt dat je daar resp. 7 en 38 sec. over doet= 45 sec. per 2 blokjes van 10 cijfers.
In 100.000 zitten 5.000 van 2 blokjes van 10 cijfers, die voor het opschrijven dus 5.000 x 45 sec. vragen.
Dat is 225.000 sec. ofwel : (60 min x 60 sec=3600 sec)=62, 5 u.
Stel dat je per dag 7 uur achter elkaar schrijft, dan ben je dus ca. 9 dagen bezig met opschrijven alleen al.
Over het optellen van 1 t/m 10 doe je 10 sec. Over 99.990 t/m 100.000 40 sec. Samen 50. Dat zijn dus ca. 10 dagen.
Dus 19 dagen heb je nodig om deze som op een ‘fysieke’ manier op te lossen; een halve minuut met je denkend vermogen.
Over de kracht van de geest gesproken!

0-0-0

[17]
Kun je met 4 vieren de cijfers 1 t/m 10 maken?

Wanneer de leerlingen alle rekenbewerkingen kennen ( 8e klas), is er met een combinatie van deze bewerkingen het antwoord te vinden op bovenstaande vraag:

Deze opgave kun je op velerlei manieren stellen:

9 geeft hier het antwoord 7
Een oplossing kan zijn: (4+ 4) + 4/4

Er zijn nog meer mogelijkheden!

0-0-0

[16]
Een plantje dat zich verdubbelt

Een mandarijn plantte in zijn tuin een wonderplantje dat zich iedere dag verdubbelde. Zijn tuin was na dertig dagen helemaal gevuld. Hij vroeg zich af hoe lang het geduurd zou hebben wanneer hij met vier plantjes begonnen zou zijn.

Oplossing:

Dat ene plantje verdubbelt zich 1 dag later: dan zijn er dus 2.
Nog een dag later – dus na twee dagen – zijn er 4.
We weten dat het vol groeien 30 dagen duurt. Met 4 plantjes beginnen neemt dus 30 – 2 = 28 dagen in beslag.

0-0-0

[15]
Met de bus naar Bussum

Deze opgave is niet moeilijk, maar je moet wel in staat zijn om vanuit de taal te begrijpen wat er gebeurt.

Twee vertegenwoordigers (twee vrienden enz) gaan met de bus naar Bussum. Slepend met hun zware koffers, gevuld met handelswaar, stappen ze één voor één de bus in. Na een kwartier vertrekt de bus om 3 uur later in Bussum aan te komen. Hoe laat is het dan?

Eén voor één is dus 1 minuut voor 1 uur. + 15 min + 3 uur.

Aankomst: 14 0ver 4.

Bij raadsels komen ook altijd de onvermijdelijke ‘het is rood en het zit in de boom’ raadsels; de meeste zijn niet echt humoristisch.

Maar af en toe komen de kinderen echt wel met humor, zoals deze (n.a.v. de bovenstaande)

Om één uur gaat er een olifant op een hek zitten. Hoe laat is het een minuut later.

Tijd voor een nieuw hek!

0-0-0

[14]
Het raadsel van Henegouwen

Het lezen van een opgave vraagt een kritische instelling. Kan het, wat wordt gevraagd. Staan er gegevens in die niet ter zake doen.

Op de weg naar Henegouwen
Kwam ik een man tegen met zeven vrouwen
Iedere vrouw had zeven zakken
Elke zak had zeven katten.
Elke kat had zeven poesjes;
Poesjes, katten, zakken, vrouwen,
Hoeveel gingen er naar Henegouwen?

Oplossing:

Ik, dus één, alle anderen kwamen juist uit de richting van Henegouwen!

0-0-0

[13]
Variant op 11

Het lezen van een opgave vraagt een kritische instelling. Kan het, wat wordt gevraagd. Staan er gegevens in die niet ter zake doen.

In iedere hoek van een 3 x 3 meter grote kamer zit een grijze kat met witte vlekjes. Bovendien zit op de staart van elke kat een kat. Hoeveel van deze poezen telt u in die kamer? En als die kamer 5 x 5 meter groot is?

Het moge al snel duidelijk zijn dat de kleur van de kat een overbodige mededeling is. Ook de grootte van de kamer is niet van belang. Het gaat dus om te beginnen om 4 katten. Maar als op de staart van iedere kat een kat zit, kun je eindeloos doorgaan. D.w.z. rekenkundig komt er geen eind. Praktisch wel: zo’n kamer is op een bepaald moment vol.
Dus in deze richting loop je vast.

Dan kan het niet anders of iedere kat zit op zijn eigen staart.

Oplossing: 4 poezen.

0-0-0

[12]
’s Werelds oudste puzzel

1. Er zijn zeven huizen en in elk huis bevinden zich zeven katten. Elke kat doodt zeven muizen en elke muis zou zeven aren spelt opgegeten hebben. Elke aar spelt zou zeven hekaten graan opgeleverd hebben. Hoeveel zijn dat er allemaal bij elkaar?

Een hekat is een inhoudsmaat van de oude Egyptenaren, ongeveer 4,8 liter.

Deze puzzel, hier vrij vertaald weergegeven, is vraagstuk 79 in de Rhind-papyrus, onze vruchtbaarste bron van de oud-Egyptische wiskunde, zo genoemd naar de Schotse Egyptoloog A. Henry Rhind, die hem in 1858 in Luxor kocht.

De Rhind-papyrus heeft de vorm van een rol van ongeveer vijfeneenhalve meter lang en drieëndertig centimeter breed, aan beide kanten beschreven. Hij stamt uit ongeveer 1650 voor Christus. De schrijver heette Ahmes, en hij verklaart dat het geschrevene een kopie is van een werk dat twee eeuwen ouder is, zodat het origineel van de Rhind-papyrus in dezelfde periode op schrift gesteld werd als een andere beroemde bron van de Egyptische wiskunde, de papyrus van Moskou, die uit 1850 voor Christus stamt.

Oplossing: 7 + 49 + 343 + 2401 + 16807 = 19607

0-0-0

[11]

Getallen 1 t/m 9 samen 100

Je hebt de cijfers 1 tot en met 9. Je mag ze alle 1x gebruiken.
De bewerking is gemengd (optellen/delen/vermenigvuldigen/aftrekken: ze hoeven niet alle 4 voor te komen)
De uitkomst is 100

8 x 9 + 1 + 2 + 3 + 4 + 5 + 6 + 7 = 100

0-0-0

[10]
Maak de cijfers rond

Een zeshoek met op elke zijde 2 rondjes. Totaal dus 12 (geen 18!) rondjes waarin je de cijfers van 1 tot en met 12 moet plaatsen. Zódanig, dat je per zijde telkens aan een gelijk totaal komt. Dus tel je per zijde de cijfers op, dan kom je steeds aan dezelfde uitkomst.

Oplossing:

0-0-0

[9]
Magisch vierkant

Vul dit vierkant aan. In dit vierkant zijn 3 hokjes van een getal voorzien. Er blijven 6 lege vakjes over. Vul nu die hokjes zo in, dat je bij het optellen van de rijen steeds dezelfde som krijgt. Zowel horizontaal als verticaal en diagonaal.

Als er geen verdere gegevens verstrekt worden, is het best lastig. Maar, als je ooit eerder met magische vierkanten hebt gewerkt, weet je dat de som van de hier gegeven kolom 15 is, dan moeten de sommen van de rijen en de diagonalen dat ook zijn. Om het makkelijker te maken kun je zeggen dat het alleen om de getallen 3, 4, 5, 6, en 7 gaat.

Oplossing:

6½ 4 4½

3 5 7

5½ 6 3½

0-0-0

[8]
Het getal 31

Elk getal heeft iets bijzonders.
Neem 31.
Speciaal is bijvoorbeeld dat je het kunt schrijven met enkel tweeën. Je moet dan weten dat 2¹ hetzelfde is als 1 x 2, dat 2² hetzelfde is als 2 x 2, dat 2³ hetzelfde als 2 x 2 x 2 en zo verder. Oh ja, en 2° is 1.
Kijk, met die manier van schrijven (die veel wordt gebruikt in
computertalen) is 31 = 2°+ 2¹+2²+2³+2⁴.
Maar misschien hou je nog steeds vooral van 3?
Ook dan is 31 een fijn getal. Je kunt het schrijven als 3/3+(3x3x3)+3. En had je algezien dat 31 een priemgetal is – een getal dat enkel deelbaar is door zichzelf en door 1? Ook daarmee kun je goochelen. Tel bijvoorbeeld de eerste 31 oneven priemgetallen bij elkaar op (2, het enige even priemgetal, doet dus niet mee). De uitkomst heeft dan weer met 31 te maken. Kijk maar: 3+5+7+11+… +83+87+ 89 = 31×31 = 31². Maar het leukste is dat 31 jaar bijna 1 miljard seconde duurt. Preciezer: iemand die 31 jaar, 251 dagen, 13 uur en ruim 11 minuten leeft, viert zijn 1 miljardste seconde op aarde.
Poeh, hoe groot zou een taart met een miljard kaarsjes wel niet moeten zijn?
Misschien is het makkelijker zo voor te stellen. Stel dat iemand vanaf de geboorte van een kind elke seconde een korrel rijst in een schuur laat vallen.

Zo’n korreltje weegt maar 20 milligram, maar ja, een miljard korreltjes samen hebben een heleboel gewicht. Hoeveel gewicht? 20.000 kilo!

Daarmee kun je een grote verjaardagsrijstmaaltijd houden! Per persoon moet je ongeveer 50 gram droge rijst rekenen, dus met 20.000 kilo rijst zou je 400.000 mensen te eten kunnen vragen, bijna een half miljoen! Tenminste, als je geld genoeg hebt voor vlees, saus
en kroepoek erbij, natuurlijk.

0-0-0

[7]
Goochelen met (priem)getallen

Vandaag is het zaterdag. Het is mei. De hoeveelste dag in mei? Nou, 1 x 2 x 3 x 4 mei. Of misschien houd je wel erg van het getal 3. Dan is het vandaag (3 x 3 x 3) -3 mei.
Wil je verschillende oneven getallen gebruiken? Dan is het vandaag 3+5+7+9 mei. En werk je graag met kwadraten (een getal maal zichzelf)? Dan is het vandaag (7 x 7) – ( 5 x 5 ) mei. De mooiste manier om 24 (want dat is het dus) te vinden, is met zulke kwadraten. Beter: met kwadraten van priemgetallen – getallen die je alleen kunt delen door zichzelf en door 1. Het gaat zo: Kies een priemgetal groter of gelijk aan 5, het maakt niet uit welk. Vermenigvuldig dat priemgetal met zichzelf (neem het kwadraat dus) en haal van het resultaat 1 af. De uitkomst is altijd een veelvoud van 24. Echt? Ja, neem 5 zelf. Daarvoor geeft dit recept: ( 5 x 5 ) 4 = 24. Inderdaad, dat is 1 x 24. Of neem 7. Dat geeft ( 7 x 7) 4 = 48, en kijk, dat is 2 x 24. En met veel grotere priemgetallen werkt het net zo goed. Neem 307: ( 307 x 307 ) 4 = 94248, en ja hoor, dat is 3927 x 24. Het is zelfs nog mooier. In plaats van 1 kun je gewoon het kwadraat nemen van een ander priemgetal – zolang dat kleiner is dan het eerste priemgetal dat je koos, en zolang ze allebei groter of gelijk aan 5 zijn.

Een goed voorbeeld is het paar 7 en 5. Dat geeft ( 7 x 7 ) – ( 5 x 5 ) = 24. Of neem 13 en 11. Dat geeft (13 x 13 )- (11 x 11 ) = 48, en hup, dat is 2 x 24.

Grote priemgetallen? Maakt niet uit. Neem 307 en 293. Dat geeft ( 307 x 307 ) – ( 293 x 293 ) = 8400, en voila, dat is 350 x 24. Kijk, dat is toch een mooi mysterie!

Wie het raadsel voor het geval van een priemgetal en 1 wil ‘oplossen’: bedenk dat elk priemgetal groter of gelijk aan 5 te schrijven is als
(6xn +1 ) of als (6xn – 1), met n een heel getal zoals 2,3,4….)

Deze opgaven stonden ooit in de zaterdagbijlage van de NRC

Of dit helemaal klopt? 6 x n=11 = 66 – 1 = 65, maar dit is geen priemgetal!
Bij de + 1 gaat het steeds op.

0-0-0

[6]
Getallenwonder

Wanneer de leerlingen niet weten wat er gebeurt, is zo’n som verrassend en raadselachtig.

Je zegt: neem een getal van 3 cijfers – niet dezelfde en geen 0.

821. Draai dit om. 128. Trek het kleinste van het grootste af. 693. Draai dit om.
396 en tel het op de uitkomst van de aftrekking: 693: altijd 1089! en bij iedereen.

Zou er na na de eerste aftrekking een getal van 2 cijfers overblijven, dan moet daarvoor een 0 geplaatst worden:

918, omgekeerd: 819. Kleinste van grootste: 99. 0 ervoor: 099. Draai dit om,
990 en tel de uitkomst van de aftrekking erbij op: 99. Uitkomst: 1089

Laat de leerlingen wat oefenen, tot ze het door hebben en nu kunnen zij bij anderen de rekenlof oogsten.

0-0-0

[5]
Optelling

De getallen 0 t/m 9 mogen 1x worden gebruikt op deze punten:

– – –
– – – +
______________
– – – –

De optelling moet kloppen:
289
764
1053

0-0-0

[4]
Emmer vullen

Een boer verkoopt losse melk, maar heeft alleen meerdere lege emmers van 3 en 5 liter staan. Iemand wil 4 liter melk. Hoe moet de boer die bepalen.

Hij vult eerst een emmer van 3 liter en gooit deze over in een emmer van 5. Vervolgens vult hij de emmer van 3 liter weer af en giet deze in de emmer van 5, tot hij vol is. Er blijft 1 liter in de emmer van 3 over. Hij pakt een andere lege emmer van 5 en giet daar de overgebleven liter in; vervolgens vult hij de 3 literemmer weer en giet deze bij de andere liter in de 5-literemmer: samen 4.

0-0-0

[3]
Kansberekening

In een zak zitten meer dan 20 ballen die 6 verschillende kleuren hebben.
Na hoeveel keer pakken weet je zeker dat je 4 dezelfde kleuren hebt.

Oplossing:

Stel dat je 6x pakt en elke kleur 1x. Zou dat 3x = 18 ballen – gebeuren, heb je alle kleuren 3 x. De 19e keer is dus een kleur waarvan je er al 3 hebt.

0-0-0

[2]
Erfenis met paarden

Een oude wijze rechter moet de nalatenschap van een rijke boer verdelen over diens 4 zonen. Deze nalatenschap omvat 39 paarden. Volgens een wet moet de oudste de helft, de tweede een kwart, de derde een achtste en de vierde een tiende deel ontvangen. Uiteraard mag er geen paard gedood worden.
De rechter weet het niet. Dan komt er een vreemdeling die hem de oplossing biedt. Die vreemdeling vertrekt daarna zoals hij gekomen is: te paard.

Oplossing:

De vreemdeling stelt zijn paard ter beschikking aan de rechter en nu heeft deze rechter er 40.
De oudste zoon de helft: 20. De tweede een kwart: 10. De derde een achtste: 5 en de vierde een tiende: 4. 20 + 10 + 5 + 4 = 39!. De vreemdeling krijgt zijn eigen paard terug.

0-0-0

breinbrekers
gewone raadsels
taalraadsels

	phawitvliet op VRIJESCHOOL – Lezen (12-6…
	Ridzerd op VRIJESCHOOL – Lezen (12-6…
	phawitvliet op VRIJESCHOOL – Lezen (12-6…
	Ridzerd op VRIJESCHOOL – Lezen (12-6…
	phawitvliet op VRIJESCHOOL – Lezen (12-6…
	Ridzerd op VRIJESCHOOL – Lezen (12-6…
	phawitvliet op VRIJESCHOOL – Sociale driegele…
	Ridzerd op VRIJESCHOOL – Sociale driegele…
	phawitvliet op VRIJESCHOOL – Is het all…
	Jolien op VRIJESCHOOL – Is het all…

VRIJESCHOOL – 6e, 7e en 8e klas – rekenen – rekenraadsels

KRAAK DE CODE

14 ? 9

30 28 13

48 39 15

HORIZONTAAL

51 X 47 + 150
6 X 710 + 2
143 X 129 + 76092
2³ X 9521
4X (6³ + 8⁴) – 2654
181² – 228
73 X 51 + 1751
(186 + 149) X (98 + 183) + 401
345 X 5²
2³X 3³X 251
(2⁶– 2) + 71 111
3 X (5124 + 6499)
5³ X (450 – 1)
20 X 70 – 43
2²X 3 X 17²

VERTICAAL

87 X 239 + 16744
25² + 6
2 X 3 X 1421
(47 + 112) X (312-129) -1504
16³ X 4 + 30
78 X 98 + 478
(983 – 718) X (38 + 225) + 1842
242² + 359
15⁴ + 13018
2²X 3 X (2147 + 3230)
3 X 38 X 40 -9
2⁴ X 2477
345 X 52 + 1
575 X 85 + 62
79 X 83- 135
5 X 113

OPlossing:

VERTIKAAL

A B
2 C X
A 4 3
5 D 0
B 8 E

2 7
2 9 x
2 4 3
5 4 0
7 8 3

803

Plaats een reactie Reactie annuleren

Follow Blog via Email

Meest recente berichten

Recente reacties

Categorieën

Blogroll

Meta

Archief

VRIJESCHOOL – 6e, 7e en 8e klas – rekenen – rekenraadsels

KRAAK DE CODE

14 ? 9

30 28 13

48 39 15

HORIZONTAAL

51 X 47 + 1506 X 710 + 2143 X 129 + 7609223 X 95214X (63 + 84) – 26541812 – 22873 X 51 + 1751(186 + 149) X (98 + 183) + 401345 X 5223 X 33 X 251(26– 2) + 71 1113 X (5124 + 6499)53 X (450 – 1)20 X 70 – 4322 X 3 X 172

VERTICAAL

87 X 239 + 16744252 + 62 X 3 X 1421(47 + 112) X (312-129) -1504163 X 4 + 3078 X 98 + 478(983 – 718) X (38 + 225) + 18422422 + 359154 + 1301822 X 3 X (2147 + 3230)3 X 38 X 40 -924 X 2477345 X 52 + 1575 X 85 + 6279 X 83- 1355 X 113

OPlossing:

VERTIKAAL

A B2 C XA 4 35 D 0B 8 E

2 72 9 x2 4 35 4 07 8 3

803

Dit delen:

Gerelateerd

Plaats een reactie Reactie annuleren

Follow Blog via Email

Meest recente berichten

Recente reacties

Categorieën

Blogroll

Meta

Archief

Ontdek meer van VRIJESCHOOL

51 X 47 + 150
6 X 710 + 2
143 X 129 + 76092
2³ X 9521
4X (6³ + 8⁴) – 2654
181² – 228
73 X 51 + 1751
(186 + 149) X (98 + 183) + 401
345 X 5²
2³X 3³X 251
(2⁶– 2) + 71 111
3 X (5124 + 6499)
5³ X (450 – 1)
20 X 70 – 43
2²X 3 X 17²

87 X 239 + 16744
25² + 6
2 X 3 X 1421
(47 + 112) X (312-129) -1504
16³ X 4 + 30
78 X 98 + 478
(983 – 718) X (38 + 225) + 1842
242² + 359
15⁴ + 13018
2²X 3 X (2147 + 3230)
3 X 38 X 40 -9
2⁴ X 2477
345 X 52 + 1
575 X 85 + 62
79 X 83- 135
5 X 113

A B
2 C X
A 4 3
5 D 0
B 8 E

2 7
2 9 x
2 4 3
5 4 0
7 8 3