.
De Zwitserse vrijeschoolleerkracht Hans Rudolf Niederhäuser schreef in de jaren o.a. 1970 artikelen over vormtekenen in het pedagogisch vrijeschooltijdschrift ‘De mensenschool’.
Ze werden in een boekje samengebracht.
.
vormtekenen
Een pedagogisch-kunstzinnige impuls van Rudolf Steiner
.
Van vormtekenen naar meetkunde
Naast al deze vrije vormoefeningen, die ook als voorbereiding voor meetkunde kunnen worden beschouwd, oefenen de verschillende klassen ook regelmatig met het tekenen van elementaire geometrische vormen: cirkels, vierkanten, gelijkzijdige driehoeken en combinaties daarvan, bijvoorbeeld twee gelijkzijdige driehoeken die elkaar snijden en een zespuntige ster vormen, een vierkant met een tweede vierkant in het midden van de zijkant, enzovoort; dan vijfpuntige sterren en vijfhoeken, zevenpuntige sterren en de zevenhoek, enzovoort.
Leerlingen moeten ook altijd ervaren hoe verschillend een driehoek, een vierkant of een vijfhoek, enzovoort, op hen werkt. Het is pedagogisch belangrijk om ervoor te zorgen dat deze vormen langdurig, tot en met klas 6, uit de vrije hand worden getekend en niet met externe hulpmiddelen. De afmetingen van de afzonderlijke lijnen worden immers niet bepaald door met een potlood of iets dergelijks te meten, maar door het gevoel voor evenwicht en harmonie te activeren, met een vrij oog. Voordat het kind leert om een cirkel te tekenen met een passer, moet het eerst leren om een cirkel te tekenen met de hand of arm in een cirkelvormige beweging.
Hierbij moet worden opgemerkt dat niet alleen de behendigheid toeneemt, maar ook de intentionele verbinding met de leerstof wordt versterkt wanneer vormoefeningen in de onderbouw ook met de voeten worden getekend. Een dergelijke intensivering van de innerlijke betrokkenheid door middel van een bevrijdende kunstzinnige onderwijsmethode is juist voor kinderen van vandaag de dag van groot belang en noodzakelijk.
In klas 5 kan de overgang van vormtekenen naar daadwerkelijke meetkunde worden gemaakt door, als een nieuwe benadering, de diverse relaties en regelmatigheden te beschouwen die voortkomen uit de getekende geometrische basisfiguren. Als er bijvoorbeeld een tweede gelijkzijdige driehoek in de driehoek wordt getekend, staand op het hoekpunt, worden door het tekenen een hele reeks geometrische relaties en regelmatigheden geactiveerd en ervaren. Deze en andere (denk aan de corresponderende driehoek getekend met een vierkant, enz.) zijn door de leerlingen in de verschillende groepen al vele malen geoefend; deze eenvoudige meetkunde, die al veel regelmatigheden bevat, bevindt zich dus als het ware in hun ledematen als vaardigheid. In klas 5 worden de geometrische regelmatigheden in de verschillende figuren waargenomen, overwogen en vergeleken. Deze worden op de eenvoudigste manier helder geformuleerd en zo bewust gemaakt.
In Nederland is de ‘meetkundeperiode’ al sinds jaar en dag een 6e-klasperiode.
Dat neemt niet weg dat in klas 5 de door Niederhäuser voorgestelde meetkundetekeningen kunnen worden gemaakt. Toen Niederhäuser zijn artikelen schreef, was het tekenen van vlechtvormen, te beginnen in klas 4 en te vervolgen in de hogere klassen, nog geen gewoonte.
Een voorbeeld: De ene dag worden twee elkaar snijdende gelijkzijdige driehoeken getekend. De volgende dag bekijkt de leerling de figuur.
Op dit niveau leren kinderen de Euclidische meetkunde dus niet synthetisch, door deze te construeren uit individuele axioma’s en stellingen; ze leiden deze af – uiteraard met hulp van de leerkracht – uit wat ze al gedaan hebben. Ze beginnen met hele getallen en leiden daaruit de elementaire wetten af die volgen. Een mentaal bewijs is op dit niveau natuurlijk niet nodig, om de simpele reden dat men simpelweg zegt wat men gedaan heeft, en zo de zaak verduidelijkt.
Dit kan heel ver leiden in de meetkunde. We willen graag het volgende benadrukken en uitwerken als een voorbeeld dat zo’n eerste waarnemings- en beschrijvingsperiode een afsluitend hoogtepunt kan zijn.
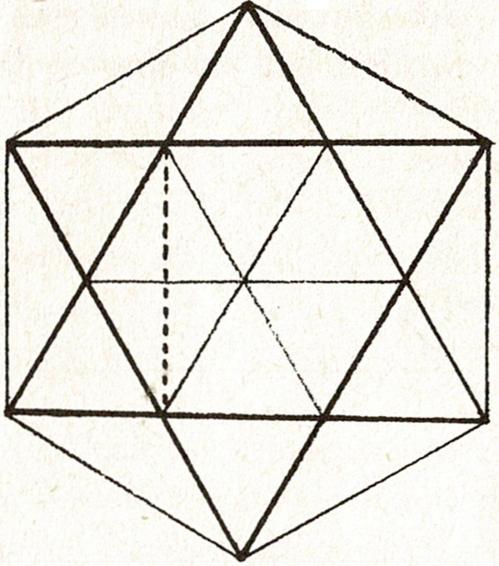
Je kan beginnen met het vierkant waarin de diagonalen zijn getekend en vervolgens de resulterende gelijkbenige rechthoekige driehoeken in alle richtingen laten uitstralen. Zie figuur 27.
Figuur 27
Zo ontstaan er ook vier kleinere vierkanten. Twee kleinere vierkanten (bijvoorbeeld rechts en links), die bestaan uit twee rechthoekige gelijkbenige driehoeken, zijn samen even groot als het eerst getekende vierkant. Het is indrukwekkend om de figuur zo te ontwerpen dat hij geopend en gesloten kan worden, zodat het gestippelde vierkant op één lijn kan worden gebracht met het eerst getekende vierkant, evenals de kleinere vierkanten enzovoort. Door deze vergelijking en observatie ben je ongemerkt aangekomen bij de wet van de stelling van Pythagoras, zij het voor het speciale geval van de gelijkbenige rechthoekige driehoek. Pythagoras is al opgenomen in de onderstaande figuur: Je hoeft alleen maar de ene driehoek te benadrukken door arcering en de vierkanten boven de katheten en die boven de schuine zijde worden meteen duidelijk als zodanig zichtbaar.
Natuurlijk kan geometrie op verschillende manieren worden ontwikkeld; het gaat er hier alleen om dit te illustreren aan de hand van een eenvoudig voorbeeld
om het basisidee te laten zien, namelijk: hoe geometrie, die uiteindelijk een hele structuur van stellingen en elkaar ondersteunende stellingen vertoont, als een gevolg uit de geometrisch actieve mens kan komen.
Op dit eerste actieve stadium moet echter een tweede, meer intellectueel en ook meer systematisch stadium volgen. Zelfs wanneer de stelling van Pythagoras voor het eerst wordt genoemd in klas 5, zoals hierboven beschreven, wordt de kinderen verteld dat het opnieuw aan de orde zal komen in klas 7 en dat ze er meer over zullen horen. Dit schept een sfeer van verwachting. Natuurlijk raakt alles wat overwogen is in de vergetelheid. Maar alleen door vergeten te worden, kan wat is opgenomen worden getransformeerd, geperfectioneerd en je eigen bezit worden. Wanneer je, misschien twee jaar later, terugkeert naar de geometrische verhoudingen die je in klas 5 hebt gevisualiseerd en ze nu vanuit een heel ander gezichtspunt benadert, komen ze uit de vergetelheid tevoorschijn. Dit verhoogt de intensiteit van de aandacht en maakt het bijvoorbeeld mogelijk om in klas 7 in korte tijd veel te begrijpen en te verwerken.
In klas 7 wordt meetkunde nu benaderd vanuit de aantoonbare kant. Dit kan op twee manieren. De bewijzen kunnen op de klassieke manier strikt vanuit de axioma’s en eerder bewezen stellingen worden opgebouwd, of de wetten kunnen worden gevisualiseerd door middel van bewegingsprocessen. Dit is waarschijnlijk de beste manier om te beginnen en de andere manier, vooral bij de complexere bewijzen, wordt later geoefend.
Het feit dat de leerlingen gedurende hun hele schooltijd euritmisch hebben bewogen – ook al deden ze dat in de middenklassen niet altijd graag – geeft hen een flexibiliteit van verbeelding en denken die het mogelijk, ja zelfs noodzakelijk maakt om deze levende verbeeldingskracht aan te spreken en zoveel mogelijk bewijzen op te bouwen uit transformerende bewegingsprocessen.
Een voorbeeld: We willen duidelijk maken dat de perifere hoeken in een halve cirkel rechte hoeken zijn.
Je gaat uit van de omtrekshoek en de middelste hoek over een kleine koorde en laat de koorde langzaam groeien; de hoeken veranderen mee. De middelste hoek wordt stomper naarmate de koorde het middelpunt nadert; de perifere hoek verliest zijn scherpte en wordt voller en voller. Als de koorde nu door het centrum gaat, wordt de middelste hoek een langwerpige hoek, de perifere hoek is een rechte hoek geworden.
Van de vele zaken die nu systematisch en zorgvuldig moeten worden opgebouwd in de meetkunde, wordt ook de stelling van Pythagoras opnieuw behandeld – om het eerder gegeven voorbeeld over te nemen en voort te zetten – maar nu in zijn geldigheid voor elke rechthoekige driehoek. Het zal de interesse van de leerlingen op dit niveau bijzonder wekken als ze gevraagd worden om zelf een bewijs te leveren en vervolgens een grote verscheidenheid aan bewijzen te zien te krijgen: de Indiase, Arabische, von Tempelhoff en natuurlijk de stelling van Euclides met zijn intellectuele structuur. Zie Steiners aanpak.
Deze veelzijdigheid is kenmerkend voor de menselijke zoektocht naar kennis. Het is niet alleen een zegen die innerlijke geruststelling en kracht geeft, het betekent ook een gezonde vorming van het intellect om steeds weer op verschillende manieren op verschillende momenten op hetzelfde terug te komen, zodat de leerlingen de stof van vele kanten leren kennen. Dit creëert een intieme band tussen de leerling en de leerstof. Als je de dingen vanuit steeds nieuwe invalshoeken en contexten leert bekijken, beginnen ze elkaar te ondersteunen en te dragen in hun waarheidsgehalte. Zo’n gevarieerde ervaring creëert een gevoel van veiligheid en vertrouwen in het denken van de leerling. Leerlingen leren voor zichzelf te denken. Dit is waardevoller dan één enkel bewijsstuk uit het hoofd te leren en het de rest van hun leven onveranderd met zich mee te dragen, als een vreemde eend in de bijt.
Met leerlingen die vanaf klas 1 bezig zijn geweest met het tekenen van meetkundige vormen en daarna, in klas 5 of zo, steeds meer aan meetkunde hebben gewerkt door ze te tekenen en te visualiseren, worden twee ervaringen opgedaan wanneer je in klas 7 of 8 overgaat op het aanpakken van meetkunde vanuit de kant van bewijzen. Ten eerste hebben deze leerlingen, vooral de meisjes, zo’n ontwikkeld gevoel voor harmonie en visualisatie dat ze de wetten meteen zien. Daarom vinden ze het vaak niet nodig om die te bewijzen.
Maar als je ze uitdaagt – en dat moet je – om uit te leggen waarom dit zo is, dan zul je in klas 7 of 8, als direct gevolg van het eerder tekenen van vormen, een beweeglijkheid en flexibiliteit van denken aantreffen die je versteld zal doen staan. Steeds weer komen de leerlingen zelf met allerlei bewijzen, waaronder de stelling van Pythagoras. Natuurlijk zijn de bewijzen die ze bedenken, afhankelijk van hun aanleg, in principe de bewijzen die ze al kennen. Het spannende is echter om te zien hoe hun intuïties opflitsen, hoe ze vaak snel de afzonderlijke stappen van het bewijs die tot de juiste oplossingen leiden, begrijpen en visualiseren, maar deze nog niet kunnen vasthouden. Het is dan de taak van de leerkracht om het idee van zo’n leerling waardoor hij het bewijs als in een flits voor zich heeft gezien, logisch met de klas op te bouwen , zodat het sluitende van het bewijs duidelijk naar voren komt uit de individuele denkstappen en kan worden overzien, of, wat niet minder interessant is, dat de onhoudbaarheid van een ander idee net zo duidelijk naar voren komt. In zulke lessen sta je met de klas heel levendig in het geheel van de meetkunde.
De oude wijsheid wordt opnieuw ervaren door de jonge zielen in vaak dramatische spanning en creatief voortgebracht uit een ondergrond van verworven kennis.
De 7e klas ervaart een nieuwe, sterke impuls, vooral door geschiedenis: de geschiedenis van de ontdekking van de aarde wordt verteld aan de hand van biografieën. Leerlingen veroveren de wereld met Columbus en Magellaan. En ze ervaren een nieuw besef van de wereld tijdens de Renaissance. Het doel is om een nieuwe dimensie in meetkundige activiteiten te begrijpen: ruimte. Het tekenen van vormen en het ervaren van vormen wordt nu getransformeerd en in dienst gesteld van het tekenen van de Platonische vaste lichamen uit de vrije hand. Ook hier is het raadzaam om niet uit te gaan van kant-en-klare modellen, hoe mooi ze ook zijn, maar om de vaste lichamen geleidelijk te laten ontstaan door uit te gaan van de kubus en het ruimtelijk voorstellen door oefenend tekenen te ontwikkelen.
Als de tetraëder, octaëder enzovoort eenmaal innerlijk begrepen en prachtig getekend zijn, is het een nieuw, speciaal genoegen om ze fysiek vorm te geven met geschikt materiaal.
Op dit moment, wanneer het doel in de meetkunde duidelijk, intellectueel begrip is, is het innerlijk gerechtvaardigd om het tekenen van vormen op een nieuwe manier te cultiveren door middel van linialen, vierkanten en passers. Het is een grote voldoening voor de leerlingen om bijzonder mooie vormen, die ze in eerdere jaren met de hand hadden getekend, te kunnen uitvoeren met instrumenten in transparante helderheid en exactheid. Als men teruggaat naar de bekende vormen, hoeven de leerlingen aanvankelijk slechts met één moeilijkheid te worstelen, namelijk de technische beheersing van het gereedschap; het materiaal is vertrouwd voor hen, maar het wordt met een nieuwe greep vastgepakt. Zo merken de leerlingen met vreugde hun innerlijke groei en rijping.
Een bijna onuitputtelijke rijkdom aan suggesties voor dit technisch tekenen, waarin het vormtekenen nu is getransformeerd, is te vinden in het werk van Prof. H. von Baravalle: “Geometrie als Sprache der Formen.” (Stuttgart 1963). (Stuttgart 1963).
De opgaven die daarin worden gesteld combineren artistiek mooie figuren met een strikt geometrische structuur van regelmatigheden in een gelukkige balans. Deze wetten worden nu veilig geoefend door herhaalde toepassing:
Door het technisch tekenen op deze manier te cultiveren, ervaren leerlingen een belangrijke relatie in het leven: dat schoonheid aan de ene kant en waarheid in de vorm van exact technisch ontwerp elkaar niet uitsluiten, maar wederzijds afhankelijk zijn.
.
Vormtekenen: alle artikelen
Meetkunde: alle artikelen
Rudolf Steiner over vormtekenen: alle artikelen
Rudolf Steiner over meetkunde: alle artikelen
Algemene menskunde: alle artikelen
Rudolf Steiner: alle artikelen op deze blog
Menskunde en pedagogie: alle artikelen
Vrijeschool in beeld: alle beelden
.
3458-3255
.
.
.
.
Alle punten die even ver van een centraal punt P liggen, vormen een cirkel
Alle hoeken waarvan het hoekpunt op de omtrek van de cirkel ligt, zgn. omtrekshoeken, zijn alle even groot, omdat ze dezelfde cirkelboog snijden.
VRIJESCHOOL 