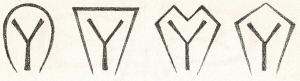Tagarchief: a-symmetrische symmetrie

VRIJESCHOOL – Vormtekenen (5-2)

Geplaatst op 9 juni 2025| Een reactie plaatsen

.

De Zwitserse vrijeschoolleerkracht Hans Rudolf Niederhäuser schreef in de jaren o.a. 1970 artikelen over vormtekenen in het pedagogisch vrijeschooltijdschrift ‘De mensenschool’.
Ze werden in een boekje samengebracht.

.

vormtekenen

Een pedagogisch-kunstzinnige impuls van Rudolf Steiner

 .

Mensvormende, kunstzinnige en methodisch-didactische aspecten

Kenmerkend voor de vrijeschoolpedagogie is, alles op een kunstzinnige manier te ontwikkelen uit wat wordend is. Bij het schrijfonderwijs wordt bijvoorbeeld niet uitgegaan van de huidige conventionele lettervormen, maar worden deze vanuit beelden ontwikkeld. Hierdoor kan het kind ervaren wat historisch is geworden. Dit methodologische principe wordt ook weerspiegeld in het feit dat meetkundelessen niet beginnen met Euclidische meetkunde in klas 7 of 8, zoals gewoonlijk het geval is. Het wordt al in de eerste schooljaren geïntroduceerd als een pure toepassing van meetkundige krachten. Op deze manier wordt geometrie als geheel niet slechts abstract ontwikkeld als een zaak voor de denkende geest, maar wordt geometrie gewekt uit de activiteit van de krachten van beweging en wil en geleidelijk verheven tot bewustzijn en helderheid van denken.

Als een kind in de eerste klas wordt gevraagd om een verticale of horizontale lijn te tekenen op het schoolbord of op een vel papier, is dat een grote inspanning voor een eersteklasser. Door te tekenen oefent hij geometriserende krachten uit die in zijn lichaam nog levend en actief zijn als vormende krachten. Het zou daarom een goed idee zijn om in de euritmieruimte te beginnen met het tekenen van vormen en de kinderen eerst de rechte lijn, de gebogen lijn, de spiegelbeeldige nevenschikking van de vormen als een bewegingsproces in de ruimte te laten ervaren. Dit zal niet altijd mogelijk zijn, maar moet vaak worden geoefend in de lagere klassen, zodat de vormen echt worden getekend vanuit de bewegende persoon.

Er is een alternatief, dat altijd gebruikt moet worden in de eerste en tweede klas en zelfs later met moeilijkere vormen: eerst de vormen oefenen met de tekenhand in de lucht, zowel de gegeven vorm als, vooral, de spiegelbeeldige tegenovergestelde vorm, en ze dan op het papierblad tekenen zodat het kind ervaart: mijn getekende lijn is de beweging die tot rust is gekomen. Als je samen met het kind symmetrieoefeningen maakt waarbij een overeenkomstige spiegelbeeldige tegenhanger wordt getekend voor een gegeven figuur, roep je, naast vele andere krachten, voortdurend zijn evenwichtskracht op, waarmee het ging staan, die het activeerde toen het leerde lopen. Dit komt in principe pas volledig tot zijn recht wanneer de vormen op het bord worden getekend dat verticaal hangt. Tekenen op het horizontale blad is een noodzakelijk surrogaat maar resulteert altijd in een illusie. In plaats van echt van boven naar beneden te ervaren, ervaart het kind alleen van achter naar voren.

Maar bij het tekenen is het kind voortdurend innerlijk aan het afwegen en meten; in het spiegelbeeldig vormen van de tegenovergestelde vorm ontwikkelt het een zeer actieve verbeelding, die zich echter nog steeds volledig wilsmatig binnen de gegeven beeldvorm beweegt en afspeelt.

De symmetrieoefeningen die Rudolf Steiner gaf voor het aanvankelijk tekenen van vormen, lijken heel eenvoudig. Maar hun vormende werking kan niet van buitenaf beoordeeld worden. Je moet al deze oefeningen steeds opnieuw ervaren om zelf te voelen en af te lezen hoe sterk en diep ze werken en stimuleren. Deze ervaring onthult ook het grote verschil tussen het tekenen van een rechts-links symmetrie met een verticale symmetrieas en een “spiegelbeeld” van de horizontale symmetrieas. Moeilijker wordt de oefening als de symmetrieas helemaal wordt weggelaten. Je moet deze verschillen in werking didactisch zorgvuldig opbouwen – in het bijzonder de afwisseling, d.w.z. het tekenen van de vorm die eerst links werd gegeven, de volgende dag aan de rechterkant en het laten afmaken aan de linkerkant, en dergelijke. En nog een nieuwe mogelijkheid voor oefeningen ontstaat door de combinatie van de twee symmetrieassen, bijvoorbeeld wanneer vrij zwevende symmetrieën worden getekend in de tweede klas met het axiale kruis. Figuur 19:

Figuur 19
.

Het is kenmerkend voor dit type vrije symmetrie dat die nog niet gevormd wordt m.b.t. het middelpunt.

Een compleet nieuwe inslag kan worden ervaren wanneer we oefeningen met centrale symmetrie ontwikkelen met de kinderen rond de leeftijd van 9 jaar. In de crisisperiode rond de leeftijd van 9 of 10 jaar, wanneer de kinderen pas echt de scheiding Ik-wereld gaan beleven, innerlijk en in de wereld, kan het belangrijk zijn om met de kinderen de cirkel te tekenen, met de opdracht in de vrij uit de hand getekende cirkel het middelpunt ervan te bepalen en, omgekeerd, om een middelpunt te bepalen en daar uit de vrije hand een cirkel omheen te vormen, vanuit de cirkelbeweging. Deze eenvoudige oefening kan worden gebruikt om een verscheidenheid aan vormen te creëren, die allemaal gebaseerd zijn op de spanning tussen de omtrek en het middelpunt. Het in- en uitwikkelen van spiralen heeft altijd een harmoniserend effect, vormen die de leerlingen ook herhaaldelijk uitvoeren bij euritmie.

Er kunnen ook centrum-symmetrische oefeningen gemaakt worden, beginnend bij de eenvoudigste, zoals hierboven aangegeven, tot de moeilijkere die Rudolf Steiner aangaf in Ilkley (op deze blog hier) en Torquay.(op deze blog hier)

De volgende oefeningen zijn ook erg stimulerend:

Probeer de cirkel niet in de gebruikelijke cirkelbeweging op papier te zetten, waarbij hij altijd als een geheel wordt ervaren, maar maak hem tweedimensionaal met breed krijt, zodat bijvoorbeeld het lichte cirkelvlak op de bladzijde wordt uitgewerkt door alles rondom het cirkelvlak in te kleuren, waardoor de cirkel van buiten naar binnen ontstaat [uitsparen] en andersom, door het cirkelvlak vanuit het midden in kleur te maken en naar buiten toe te laten groeien. Het is ook aantrekkelijk om de bekende verticalen en horizontalen of andere geometrische vormen (vierkant, ruit enzovoort) opnieuw te maken en te ervaren.

Als het tekenen van cirkels en centrale symmetrie hier in het bijzonder wordt benadrukt in de context van de crisis rond het 9e, 10e jaar, dan is dit niet bedoeld als een dogma dat men voor die tijd geen cirkels zou mogen tekenen! Dat kan en moet zeker. Maar het is ook belangrijk om te onderscheiden wanneer een oefening een bijzonder wakker makend accent heeft in de context van de ontwikkelingsfase van het kind en in staat is om dit te bieden; zo’n moment moet in het bijzonder worden benut.

Het is een heilzaam principe, omdat het volkomen onintellectueel is, dat een en dezelfde oefening steeds opnieuw gedaan kan worden in verschillende leeftijdsgroepen, ook in variaties, en daarbij steeds nieuwe aspecten kan ervaren. Denk maar aan verticaal tekenen, wat zeker niet beperkt is tot het eerste schooljaar. Het oefenen van verticalen en horizontalen is altijd nieuw, het blijft altijd een inspanning. Verticalen, horizontalen, cirkels, de geometrische basisvormen in het algemeen, zijn levende archetypen, geschikt om geometrische krachten te stimuleren en te activeren in bekende en steeds nieuwe vormen door alle schooljaren heen.

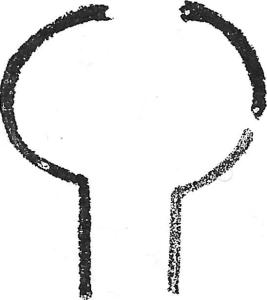
In de oefeningen die Rudolf Steiner in Ilkley en Torquay gaf, waarbij innerlijk en uiterlijk, uiterlijk en innerlijk met elkaar moeten corresponderen, komt een geheel nieuw element aan de orde dat veel verder gaat dan centrale symmetrie. Rudolf Steiner noemt het “innerlijke” symmetrie waarbij het volledig afhangt van het ervaren van de spanning tussen de innerlijke en uiterlijke krachten en vice versa. Het zou ook dynamische symmetrie genoemd kunnen worden, omdat niet de parallel lopende evenwichtsbeweging van de binnenste en buitenste cirkels belangrijk is, zoals in figuur 2, [zie deel 1]

maar hun gespannen tegenbeweging, hun vrije spel rond een waargenomen cirkelvormige lijn. Dit creëert harmonie door intensivering. Deze oefeningen zijn bijzonder geschikt voor het ontwikkelen van levendig denken en verbeelding.

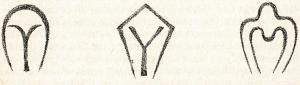
Oefeningen van inversie, omkering en metamorfose zijn ook bijzonder geschikt voor de vorming van een flexibele verbeelding, een levend intellect. Ze kunnen met enige voorzichtigheid gebruikt worden, zelfs met 1e-klasssers, als je er rekening mee houdt dat een eenvoudige symmetrieoefening om van de linker- naar de rechterkant te gaan of zelfs om te keren de volgende dag, een diepgaand effect heeft en  de etherische krachten stimuleert (Figuur 20):

Figuur 20
.

Met dit element van omkering kan op vele manieren gespeeld worden zonder verwarring te veroorzaken, zodra de kinderen enig vertrouwen hebben gekregen in de elementaire symmetrie-oefeningen.

Rudolf Steiner gaf in Oxford en Dornach eenvoudige veranderoefeningen  voor het borduren van een jurk.7 (Figuur 21.)

figuur 21

aan de hals

op de ceintuur

aan de zoom

Dornach (op deze blog hier)
GA 303/261-264
Vertaald/293-296

aan de hals

op de ceintuur

aan de zoom

Oxford (op deze blog hier)
GA 305/137-143
Vertaald/127-133

Deze ontwerpen kunnen worden gebruikt bij het vormtekenen en kunnen tot nieuwe stimuleren in de zin van dit principe van transformatie.

In een eerste en tweede klas kunnen innerlijke flexibiliteit en soepelheid van verbeelding worden ontwikkeld door middel van de volgende oefeningen: figuur 22 en 22a.8:

Figuur 22
.

Schilder de oefening in twee kleuren zodat deze veel sterker ervaren kan worden, bijvoorbeeld groen aan de binnenkant en rood aan de buitenkant, of geel en blauw. In dit rood (sterke lijn) (Figuur 22a):

Figuur 22a
.

leeft een dringende kracht die steeds meer naar boven duwt. Uiteindelijk is wat groen was aan de binnenkant (stippellijn) de buitenkant geworden en is het rood aan de buitenkant (ononderbroken lijn) de binnenkant geworden. In deze oefening heeft het kind een inversie in zijn eenvoudigste vorm ervaren, die tot jubelend enthousiasme leidt zodra het zich dit realiseert.
(Deze figuren ontwikkelde Willy Maetzke in Zürich met zijn klas)

Een ander voorbeeld van een metamorfose (figuur 23):

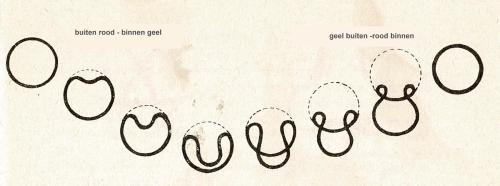Figuur 23
.

Met oefeningen als deze bevind je je in een krachtenrijk dat de mooiste voorbereiding is op de lessen plantkunde in de vijfde klas, voor een levendige observatie van de natuur in het algemeen die zich inleeft in de krachten die aan het werk zijn.

Om de verbeelding van de leerkracht te trainen en een flexibele verbeelding te ontwikkelen, verwijzen we naar een boek van Louis Locher-Ernst: “Einführung in die freie Geometrie ebener Kurven.” Het bevat een stimulerende rijkdom aan metamorfosen, evenals vormen en hun tegenvormen, ontwikkeld vanuit een artistiek-wiskundige benadering. We nemen drie voorbeelden uit het boek (figuren 24 en 25) om te illustreren waar het om gaat: het eerste van negen paren metamorfosen.

Figuur 24
.

vorm                                                                         tegenvorm

Dergelijke vormen en tegenvormen, aanvankelijk alleen getekend, kunnen vervolgens wiskundig worden geconstrueerd op bovenbouwniveau. De leerlingen hebben dan al de nodige vrije verbeelding.

Figuur 25
.

Met al deze figuren kan de dynamiek van de omvorming ook op een eenvoudige verbeeldende manier begrepen worden, waardoor de motieven ook door negenjarigen getekend kunnen worden.

De volgende omstulpingsoefening, figuur 26 (naar Prof. F,Zaunert, Schaubilder kmplexer Funktionen, Beilage zu, 3. Jahresbericht der Bundeshandelsakademie A-Villach 1970-1971
Figuur 26
.

kan in de benedenbouw vooreerst uit het beleven van de symmetrie getekend worden en in de bovenbouw wiskundig constructief begrepen worden.
Het ervaren van zulke herhalingen en intensiveringen, ook al zijn die over jaren verspreid, is een zegen voor de opgroeiende mens. Hij voelt aan markante  punten hoe de presentatie van inhoudelijke kennis in een organische opbouw en samenhang staat; hij ervaart als een stemming van de ziel hoe kennis en inzicht een psychisch-spiritueel groeiproces is, in staat tot voortdurende verdieping en toename.

                                                                        *
5e klas

Voor het vijfde leerjaar geeft het leerplan aan dat de kinderen kennis moeten maken met de Griekse cultuur in mythe, legende en geschiedenis. Om deze onderdompeling in de Griekse cultuur te ondersteunen, kunnen verschillende oefeningen in vormtekenen worden gemaakt, die allemaal op de een of andere manier gebaseerd zijn op het principe van de naar binnen en naar buiten zich bewegende spiraal, een vormelement waarmee de Griekse verbeeldingskunst onuitputtelijk speelde. (Figuur 27.):

Figuur 27
.

Figuur 28 toont een oefening met een prachtig harmoniserend effect, vooral als je de weggetjes meerdere keren doet: het gaat van de binnenste, kleinste spiraal naar de buitenste, grootste. Deze polariteit bepaalt de grootte van de vorm bij de eerste beweging. De verdere ontwikkeling leidt door een willekeurig aantal  trappen over de balans naar de omgekeerde spanningsverhouding tussen binnen en buiten:

Figuur 28
.

Als we uitgaan van spiralen, hebben we altijd een binnenvorm (dubbele, drievoudige of viervoudige spiraal in zwevende symmetrie), waarna de taak ontstaat om eenvoudige, passende omhulsels te maken. (Figuren 29 en 30.)

Figuur 29
.
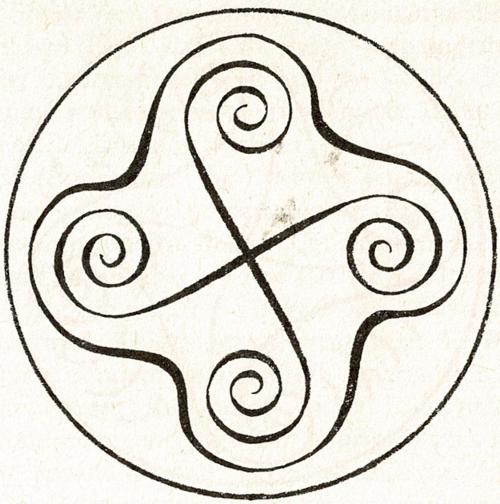Figuur 30
.

Er kan ook een band worden gemaakt uit de inwikkelende- en uitwikkelende spiraal (figuur 31), dat dan verdere toevoegingen nodig heeft als afsluiting (boven en onder).

Figuur 31
.

Opdracht voor zelfstandig ontwerpen is om de leerlingen dit motief in een hoekige vorm te laten gieten. Het is ook stimulerend om symmetrieën te creëren op basis van opsmuk en schildvormen uit de zogenaamde Schat van Agamemnon (Nationaal Museum in Athene) te laten tekenen (figuur 32 a + b)- door alleen de binnenvorm aan te geven en de leerlingen dan de omsluitende afsluiting te laten zoeken en bedenken, en dan wellicht ook de klassiek overgeleverde vorm te laten tekenen.

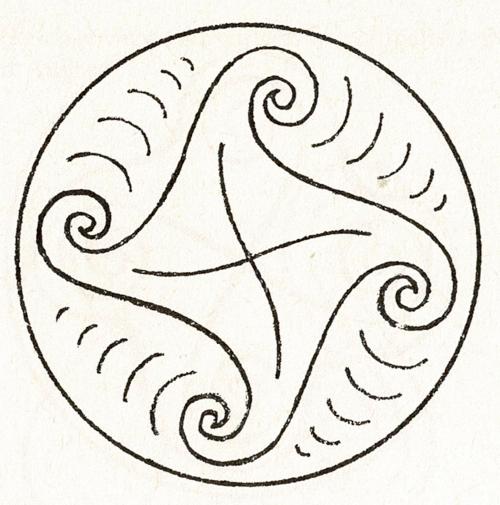Figuur 32

.

Figuur 32A
.

Voor zover de kinderen via het tekenen een intiemere band kunnen krijgen met de Griekse vormentaal, is het gerechtvaardigd om zich te laten inspireren door Griekse ornamentele motieven. We hebben echter een grens bereikt. We kunnen het gevaar van verstarring dat hier dreigt door het louter kopiëren van historische vormen vermijden als we de vormen niet namaken, maar ze in plaats daarvan vrij en opnieuw scheppen vanuit hun dynamische stijl, vanuit het element beweging. Dan benaderen we het ontstaansmoment waaruit ze oorspronkelijk voortkwamen. Ze zijn allemaal, zowel de Griekse als de vlechtvorm-bandmotieven uit de Noords-Germaanse cultuursfeer, oorspronkelijk ontstaan uit de ervaring en waarneming van de etherisch stromende, bewegende vormenwereld, en deze etherische stromingen werden vervolgens vastgehouden als als ornamenten.

In deze zin kan bijvoorbeeld de euritmische oefening: samengaan en uit elkaar gaan (ballen und spreizen], gebruikt worden om op de meest eenvoudige manier een knop-bloesem motief te ontwikkelen, dat heel expressief gekleurd kan worden in de polariteit blauw-violet-geel-rood. De eenvoudige vormentaal onthult veel verwijzingen naar het leven. (Figuur 33.)

Over het ontstaan van het palmettenmotief (gestileerde ornamenten die een rechtopstaand blad opgedeeld in lobben vertonen, zoals een waaier of palmblad. Gebruikelijk in klassieke en neo-klassieke stijlen, individueel of samen met andere gestileerde bloem of bladvormen in een anthemion gebruikt) en andere ornamente zie de voordracht Rudolf Steiner van 7  juni en 28 juni 1914, in: GA 286.. Über das Akanthusblatt siehe auch: F. Kempter: «Akanthus – Die Entstehung eines Ornamentmotivs»,

Dit motief komt vaak voor in de Griekse kunst. Wij hebben echter een geheel nieuwe manier bedacht om het vorm te geven.

Op dezelfde manier kan een ornamenteel motief worden ontwikkeld uit de beweging van twee lijnen, een bovenste en een onderste, die deels parallel lopen, deels in parallelle tegenbeweging; hun ritme verschuift en schommelt in de derde weer analoog aan de eerste.
Deze oefening is ook gebaseerd op een soort asymmetrische symmetrie. (figuur 1 en 3; 2 en 4 corresponderen met elkaar. Figuur 33a.)

Figuur 33A
.

Door de dynamiek van de beweging opnieuw te ervaren (omhoog-omlaag, rechts-links, etc.), kom je tot het ontwerp van dit traditionele motief en creëer je het opnieuw.

★

Nu komen weer andere kanten en krachten aan bod door vlechtvormen te tekenen, die je bijvoorbeeld in de 4e klas kan nemen om daarmee aan te sluiten op de verhalen uit de Noords-Germaanse mythologie, heldensagen en cultuur.

Binnen de Keltisch-Germaanse, Ierse, maar ook Lombardische culturen vind je een verscheidenheid aan suggesties die vrij kunnen worden omgevormd tot een vormoefening of nagedaan kunnen worden. (Figuur 34.)

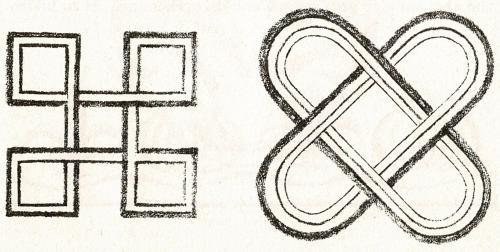Figuur 34
.

Als een geheel nieuw element zoals de vlechtvormen moet worden begrepen, is het raadzaam om te beginnen met eenvoudige oefeningen die al eerder zijn getekend om het nieuwe element te ontwikkelen, bijvoorbeeld een soort staf van Asclepius of drie cirkels. (Figuur 35.)

Figuur 35
.

Deze eerste oefening kan nu zo worden gedaan, dat op het snijpunt altijd één lijn door de bovenkant en de andere door de onderkant wordt getrokken. In het eerste moment ben je vrij om te kiezen; als je eenmaal hebt besloten, zijn alle andere snijpunten, bijvoorbeeld die van de drie cirkels, bepaald; het is nu een kwestie van intellectuele overweging, die niet abstract, maar tegelijkertijd levendig met de tekenhand wordt uitgevoerd.

Een vijfdelige vorm, variërend naar buiten, naar binnen, rond of hoekig (figuur 36), biedt mogelijkheden om zeer vaardige leerlingen opdrachten te geven die ze zelfstandig kunnen oplossen.

Figuur 36
.

Hetzelfde motief kan ook in drie of vier delen worden aangepast
(Figuur 37)

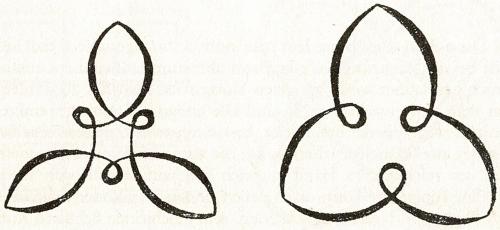Figuur 37
.

Deze vormen (figuren 36, 37) kunnen ook worden opgevat als nog niet helemaal af; de leerlingen voelen zich uitgedaagd om een geschikte definitieve omsluitende vorm te vinden. Op deze manier wordt het principe van “perfectioneren van het onvolmaakte” op steeds nieuwe manieren herhaald.

Het tekenen van zulke ingewikkelde vlechtmotieven daagt eigenlijk het vermogen uit om te differentiëren en te onderscheiden – echter niet conceptueel en intellectueel, maar puur als behendigheid van de vingers als het gaat om het tekenen van zo’n vlechtmotiefmotief, geschetst in prachtige kleuren, op zo’n manier dat het afwisselend boven en onder wordt doorgetrokken. Zulke en ook ingewikkeldere vlechtvormen wekken onderscheidingsvermogen – slimheid – op tot in de vingertoppen. Maar de hele mens is er nog steeds bij betrokken. Deze fijn differentiërende activiteit van de tekenhand heeft een wakker makend effect op het denkende hoofd.

Het motief van vlechten is zeker niet voorbehouden aan de 4e klas. In deze klas heeft het echter een gezond vormend, revitaliserend en wakker makend effect op het intellect, dat zich als het ware nog in de ontluikende fase bevindt. Voor hogere klassen kunnen altijd nieuwe gezichtspunten worden ingenomen, andere wetmatigheden worden uitgewerkt.

We verwijzen hier maar het stimulerende werk van Rudolf Kutzli over de Lombardische vlechtmotieven 

Het kan bijvoorbeeld een goede oefening zijn in het disciplineren van het denken en de wilskracht voor een negende klas als de leerlingen in het technisch tekenen een ingewikkelder lintmotief precies en verzorgd ontwerpen met passer, liniaal en pen en inkt.

Zoals reeds vermeld bij de Griekse motieven, ligt ook hier de verleiding op de loer om te eenzijdig betrokken te raken bij de loutere reproductie van dergelijke historische vlechtmotieven. In onze context kan het echter niet gaan om de introductie van een renaissance van Griekse ornamenten of banden. Maar het principe van ineenvlechten of weven moet zeker worden toegepast en gebruikt   voor de gedachtevorming in de 4e klas. Maar in plaats van uit te gaan van traditionele motieven, die als afgewerkte, voltooide objecten altijd de neiging hebben om te stollen, is het raadzaam om uit te gaan van een echt verband, bijvoorbeeld de eerste fase van het strikken van schoenen, en de kinderen dit te laten tekenen. Door te tekenen worden de kinderen zich bewust van een activiteit die ze misschien al duizend keer met hun handen hebben gedaan. Een belangrijk bewustwordingsproces voor de vierdeklassers. Of, in samenwerking met de handwerklerares, laten we de kinderen het weefsel tekenen van een riem die ze geweven hebben met gekleurde wollen draden, of het vlechten dat ze doen bij het breien, haken of macramé maken. (Afbeelding 38.)

Figuur 38
.

Kutzli ontwierp een leergang voor het leren tekenen van vlechtvormen.
Op essentiële punten wijken zijn opvattingen af van die Niederhäuser haar voorstelt. 
In het kort: niet nadoen van voorbeelden, zoals hierboven, maar na de vorm goed in je op te hebben genomen, uit de herinnering de kruisingen ‘onder en boven’ uitvoeren.
De tekening hierboven is geen ‘echte’ vlechtvorm, want op bepaalde plaatsen wordt de stroom ‘door-stop’ onderbroken.
Dat neemt niet weg dat het kijken naar deze vormen, ook zijn nut kan hebben, bv. als concentratieoefening

En in plaats van een historisch overgeleverd drakenmotief over te trekken, moedig je de kinderen aan om zo’n vervlochten structuur, harmonieus in balans, vrij te creëren vanuit hun eigen verbeelding. Hun eigen creatieve activiteit! Als dat dan, zoals bij handvaardigheid kan worden gedaan, leidt tot kleine bruikbare voorwerpen (onderzetters geweven met touwtjes, etc.), dan is er een onschatbare bijdrage geleverd aan het levendig, realistisch oefenen van het denken.

De nadruk leggen op dergelijke taken ligt in lijn met de geest van de opvoedingskunst die door Rudolf Steiner werd geïnitieerd. Dit herhaalt slechts op een ander gebied wat hij stelde als een beslissend principe voor het onderwijs in schrijven: Niet uitgaan van wat geworden is, maar van wat aan het worden is.

★

Een paar opmerkingen over het kleurontwerp van de vormtekeningen moeten hier worden toegevoegd.

Het is gemakkelijk om het ideaal te formuleren dat schoonheid ligt in de harmonie van de vormen met de gekozen kleuren. Maar afgezien van een paar geslaagde pogingen ontbreekt het ons meestal nog aan een zeker zintuiglijk-ethisch gevoel voor de taal van vorm en kleur. In deze verlegenheid beslist iedereen volgens zijn eigen persoonlijke smaak. Als je de kinderen hun eigen kleuren laat kiezen, zul je in elke klas individuen vinden die met kalme zekerheid zulke eenvoudige, gelukkige oplossingen vinden dat ze de hele klas kunnen inspireren; bij de meesten wordt het echter te willekeurig en te kleurrijk.

In welke richting moet men leiden?

Het lijkt ons dat het karakter van de vorm als een beweging die tot rust is gekomen niet moet worden uitgedoofd door het kleuren, maar dat het karakter van de beweging van de vorm juist moet worden benadrukt en uitgewerkt door de kleur. Gekleurd papier waarop de vorm fel is weergegeven met bijpassende kleuren zou erg mooi zijn. Als je wilt dat de kinderen het vel inkleuren, moet je hun activiteit zo sturen dat de vorm duidelijk door de gekleurde achtergrond heen te zien is. Om dit te doen, is het aan te raden om de waskrijtjes plat op het papier te leggen of hiervoor waskleurblokjes te gebruiken, omdat je hiermee heel breed kan kleuren met ‘laagjes.’ [Duits: lasieren]

Bevredigende oplossingen kunnen worden bereikt door de kinderen aan te moedigen om de vormen bijvoorbeeld met een lichter blauw te tekenen en ze dan over te trekken met een donkerder blauw (aan één kant) of om andere kleurenparen te kiezen. In de 4e of 5e klas komen de leerlingen zelfs op het idee om de vorm in het wit te tekenen en het oppervlak eromheen in laagjes te kleuren met een donkerdere en lichtere kleur, waardoor een mooi en duidelijk vormeffect ontstaat. Het lijkt ons dat de manier die we vaak in de klas tegenkomen tegen de zin van het vormtekenen ingaat: dat de kinderen met enorme vlijt in regenboogkleuren, herhalende strepen of iets dergelijks om de vorm heen tekenen, in bewegingen die absoluut niets met de vorm te maken hebben, maar ook niet met de essentie van de kleur.

Wat het vormtekenen in z’n algemeenheid betreft, zou je moeten zeggen dat het toch in de allereerste instantie gaat om oefenen, oefenen, oefenen. (Zie bv. Algemene menskunde 4 (4-4).
Wanneer een vorm ‘zit’, m.a.w. ‘gekend’ wordt, is het element van oefenen voorbij. Een heel mooi gelukte wat de vorm betreft, zou dan – met bovenstaande in acht genomen – gekleurd kunnen worden. Dan is het met kleur een mooie afronding. Maar geen doel op zich.
(De vele voorbeelden op Pinterest suggereren dat het om de mooi gekleurde vorm gaat, om dit resultaat.)

Het is niet alleen gerechtvaardigd, maar ook noodzakelijk om de kinderen de gewoonte bij te brengen dat er zorgvuldig en met aandacht aan de uitwerking gewerkt moet worden; maar dat dit kleurrijke ontwerp  ingetogen moet zijn en in overeenstemming met het doel van het werk. Het is maar al te gemakkelijk om “inkleuren” te laten ontaarden in nietszeggende speelsheid, zelfs in maniërisme, wat niet alleen tijdverspilling is, maar nog veel erger: een misbruik van wat bedoeld wordt met het artistieke, en wat we bij kinderen willen opwekken als een gevoel voor het verschil tussen kleur bij schilderen en lijn bij vormtekenen; want door zo’n inkleuring wordt geweld gedaan aan zowel de vorm als vooral aan de kleur.

Gelukkig is in de stenografische transcripties van de Ilkleyvoordracht informatie over de kleuren die Rudolf Steiner gebruikte in zijn vormtekeningen toegevoegd aan de schaars aangegeven schetsen: oranje en blauw.

Hij gebruikte oranje voor de symmetrie lijn (figuur 1) en blauw voor de gebogen lijn. Hij koos deze kleuren ook (we weten niet of dit opzettelijk was of dat hij geen andere geschikte kleuren tot zijn beschikking had) voor de figuren 2 en 4: hij tekende de binnenvorm van figuur 2 in oranje en de omhullende buitenvorm in blauw; voor figuur 4 veranderde hij de kleur en gebruikte blauw voor de binnenvorm en oranje voor de buitenvorm. Helaas ontbreken de kleuren in figuur 5 en 6. Dit is niet veel, maar het geeft wel een duidelijke richtlijn. We kunnen hieruit verschillende suggesties afleiden voor het kleurontwerp:

Duidelijk en eenvoudig; complementaire kleuren voor binnen en buiten; omkering van de kleuren in metamorfoses; de kleuren benadrukken de kenmerken van de vorm (binnen-buiten, actief-passief) en maken tegelijkertijd hun innerlijke verbinding (omkering) duidelijk. (Zie ook de kleurkeuze bij de temperamentsoefeningen in de seminarcursus).

GA 295/32  in de gedrukte versie
Praktijk van het lesgeven/32

Deze paar details laten zien hoe de kleur welsprekend kan worden gebruikt om de vorm te benadrukken in zeer verschillende opdrachten. Ze geven de leraar suggesties voor creatieve experimenten, geven hem alle vrijheid en leiden zachtjes de vleugels van zijn verbeelding zodat hij niet te ver afdwaalt van de essentie.

Deel 1       deel 3     deel 4     deel 5

.

Vormtekenen: alle artikelen

Rudolf Steiner over vormtekenen: alle artikelen

Algemene menskunde: alle artikelen

Rudolf Steiner: alle artikelen op deze blog

Menskunde en pedagogie: alle artikelen

Vrijeschool in beeld: alle beelden

.

3448-3246

.

.

.

Een reactie plaatsen

Geplaatst in vormtekenen

Getagged , , , , , , , , ,

VRIJESCHOOL – Vormtekenen (5-1)

Geplaatst op 1 juni 2025| Een reactie plaatsen

.

De Zwitserse vrijeschoolleerkracht Hans Rudolf Niederhäuser schreef in de jaren o.a. 1970 artikelen over vormtekenen in het pedagogisch vrijeschooltijdschrift ‘De mensenschool’.
Ze werden in een boekje samengebracht.

.

vormtekenen

Een pedagogisch-kunstzinnige impuls van Rudolf Steiner

Voorwoord

Vandaag de dag leven we in de traditie van een rijke vormencultuur.
De vormen die we terugvinden in de decoratieve kunst op alledaagse voorwerpen, op gereedschappen en wapens, sieraden, rituele gebruiksvoorwerpen, etc. werden in de oudheid gecreëerd door alle volkeren die min of meer onbewust en naïef leefden in de perceptie van een wereld van vormen en een taal van vormen die geweven en gevormd worden door de vormscheppende geesten in het rijk van de levenden. In dit rijk van levende vormen is alles wat zich in de natuur en in de ware kunst in zichtbare vormen verdicht archetypisch.

Deze perceptie van de levend-scheppende wereld van vormen vervaagde in die mate dat mensen ontwaakten tot het aardse bewustzijn van objecten, en de wereld van technologie op aarde creëerden volgens maat, aantal en gewicht, volgens aspecten van doelmatigheid. De oorspronkelijk levende vormcreatie stierf uit, stolde en werd alleen doorgegeven als een mooie, zij het dode, traditie.

In deze situatie rijst de vraag: Kan de toegang tot de levende ervaring van vorm en de creatie van vorm teruggevonden worden?

Een eerste stap naar een nieuwe artistieke creatie en ervaring hebben we te danken aan Goethe. Hij vestigde de aandacht van de schilderende kunstenaar op de zintuiglijke en morele ervaring van de wereld van kleur, waardoor – na de duisternis van het materialisme – de eenheid van kleur en mens kan worden hervonden. Wat Goethe illustreerde voor de ervaring van kleur geldt voor alle kunsten en hun uitdrukkingsmiddelen.

De tweede stap hebben we te danken aan Rudolf Steiner, die met de bouw van het eerste Goetheanum in Dornach niet alleen een opleving, maar ook een vergeestelijking van alle kunsten inluidde.

Deze Goetheanum-kunst, bijvoorbeeld in de zegeltekeningen voor zijn mysteriedrama’s, is ook de bron van de impuls die Rudolf Steiner in 1919 in de vorm van het beleven en tekenen van vormen in het leerplan van de vrijescholen in Stuttgart opnam. Door dit tekenen van vormen kan het opgroeiende kind toegang tot het gevoel van de levend-scheppende wereld van vormen worden geopend, gerevitaliseerd en versterkt door oefening.

De leraar moet deze toegang echter bewust ontwikkelen door te oefenen vanuit de ervaring van de zintuiglijke en morele taal van rechte lijnen, rondingen, symmetrie en geometrische basisvormen. Hij moet ze ervaren als een proces van beweging dat tot rust is gekomen in de getekende vorm. Door deze vormen te tekenen, doet hij het begraven, maar ook sluimerende gevoel voor de wereld van vormen, herleven en ontwaken. Dit is een eerste bescheiden begin van een nieuwe artistieke creatie.

Vanuit dit gerevitaliseerde gevoel voor vorm en vormcreatie, waardoor onder andere een nieuwe levendige waarneming en herkenning van de natuur wordt gestimuleerd, kan ook een nieuwe benadering worden gevonden van de prachtige vormen die ons zijn overgeleverd uit oude volksculturen.

Antroposofie laat de mens zichzelf ervaren als een eeuwige individualiteit met een eigen bestemming, die herhaalde levens op aarde doormaakt, en laat hem zichzelf ervaren als een verbindende schakel tussen aarde en kosmos. Antroposofie laat de mens ook de edele krachten in het leven van de volkeren ervaren, waardoor zich over de hele aarde zo’n levendige en wonderbaarlijke verscheidenheid van cultuur openbaart als uitdrukking van de ziel van deze volkeren. Alleen door de waarneming van deze veelvormige schepping van vormen en cultuur wordt het wezen van de mens in zijn totaliteit en veelvormige taak op aarde volledig zichtbaar.

Hans Rudolf Niederhäuser

Inleiding

Met euritmie en vormentekenen heeft Rudolf Steiner iets in het moderne schoolprogramma geïntroduceerd dat tot dan toe nog niet eens als aanwijzingen bestond.

Wie zich verdiept in de aard en de werkwijze van euritmie en vormtekenen, ontdekt dat kunstzinnige opvoedingsmiddelen een versterkende en helende werking hebben op de kinderen, zodat ze innerlijk gesterkt worden om de eisen die het moderne leven aan mensen stelt, te kunnen weerstaan.

De kinderen oefenen euritmie in een of twee lessen per week gedurende hun hele schoolleven; vormtekenen begeleidt hen van jaar 1 tot 5*; het wordt meestal twee of drie keer per jaar gedurende twee of drie weken in het hoofdonderwijs geoefend, maar kan ook per uur gedurende het hele jaar worden geoefend.

Als je de kinderen vertelt dat een periode van vormtekenen gaat beginnen, juichen ze en worden ze enthousiast. Vormtekenen vervult duidelijk een van de diepste behoeften van het kind. Door het actief creëren en vormgeven van vormen, wordt het in staat gesteld zichzelf op te voeden; het wordt in staat gesteld volledig te leven in het creëren en doen, maar op zo’n manier dat het zichzelf niet uitput in het proces, omdat het in het creëren ook altijd de andere polariteit mede-activeert en ontwikkelt, zelfs als deze verborgen is: die krachten die later in het kind opbloeien als denken.

We zullen eerst een samenvatting geven van de aanwijzingen die Rudolf Steiner op verschillende plaatsen en tijden over vormtekenen heeft gegeven. Daarna staan we stil bij enkele methodologische en didactische aspecten, bekijken we de vormtekening als voorschool van de meetkunde en traceren we in het laatste deel de vele, soms verborgen, verwante relaties en gevolgen van de vormtekening.

In de voorstelling moeten we afzonderen en verenigen wat in werkelijkheid samenwerkt. Aan de andere kant is het niet te vermijden dat we soms weer op iets terug moeten komen en herhalen om de veelheid aan wat met elkaar te maken heeft en elkaar overlapt, aan te geven.

1.Aanwijzingen van Rudolf Steiner

Voor zover bekend heeft Rudolf Steiner drie keer aanwijzingen gegeven over vormentekenen en telkens nieuwe, kenmerkende elementen ontwikkeld. Met een beetje fantasie kunnen deze aanwijzingen gebruikt worden om een didactische structuur op te zetten voor klas 1-5 tot aan het punt waar het eigenlijke meetkundeonderwijs begint. Rudolf Steiners aanwijzingen belichten heel verschillende aspecten van vormtekenen, maar ze sluiten elkaar niet uit; ze hoeven alleen maar samen gezien te worden, dan vullen ze elkaar aan en doordringen elkaar.

Rudolf Steiner gaf de eerste elementen van vormtekenen in 1919 in Stuttgart ter gelegenheid van de basiscursussen voor leraren:

[1] GA 293
Algemene menskunde als basis voor de pedagogie
[] GA 294
Opvoedkunst. Methodisch-didactische aanwijzingen
[] GA 295
Praktijk van het lesgeven

In het derde en vierde seminargesprek, op 23 en 25 augustus, sprak Rudolf Steiner voor het eerst over vormtekenen. Hij karakteriseert het hier als een middel tot temperamentsopvoeding. Samen met de deelnemers, de toekomstige leraren van de eerste vrijeschool, werkt hij vormen en kleurtinten uit voor de verschillende temperamenten en laat hen elk de tegenovergestelde vorm tekenen.
Dit is op deze blog uitvoerig uitgewerkt bij ‘temperament en rekenen‘ waarin de vormtekeningen a.h.w. een uitgangspunt vormen voor de 4 rekenbewerkingen.

In de eerste les, adviseert Rudolf Steiner in de 4e voordracht van ‘Opvoedkunst, de leraar de kinderen naast bepaalde kleuroefeningen een rechte en een kromme lijn op het bord te laten tekenen. In de genoemde lezing karakteriseert hij ook de waarde en pedagogische betekenis van deze oefening in termen van het vestigen van een gevoel van autoriteit.
Zie ‘Rudolf Steiner in de 1e klas‘ en alle overige artikelen die de rechte en de ronde/kromme tot onderwerp hebben.

Deze eenvoudige lijntekeningen en hun herhaling en het onthouden van de concepten de volgende dag maken een onuitwisbare indruk op de kinderen.

Vanuit het oogpunt van vormentekenen is het vermeldenswaard dat Rudolf Steiner in deze vormen – die nog niets te maken hebben met de latere symmetrie-oefeningen – van meet af aan de twee polaire vormprincipes laat maken en beleven: de rechte, stralende lijn en de gebogen lijn; de eerste als uitdrukking van de wil, de tweede als uitdrukking van het denken, gezien vanuit het gezichtspunt van de ziel. Vastleggende eenzijdigheid kan worden vermeden als deze polariteit van het ronde en het rechte in alle vormen afwisselend wordt gehanteerd.

In zijn werk “Harmonicus Mundi” schrijft Johannes Kepler over deze vormende polariteit van de wereld, die de eersteklasser al in de eerste les door het doen ervaart: “dat God in zijn onwrikbare raad vanaf het begin het rechte en het kromme heeft gekozen om de goddelijkheid van de Schepper in de wereld in te tekenen”. En op een andere plaats: “… Zo heeft de Alwijze de wereld van het grootse bedacht, waarvan de hele essentie besloten ligt in de twee verschillen van het rechte en het kromme.”

In verband met het schrijfonderwijs en de inleiding in de meetkunde spreekt Rudolf Steiner in deze vakken herhaaldelijk over het tekenen van vormen. In de tweede leerplanvoordracht (6 september 1919) vat hij een aantal punten samen die in de tekenlessen voor leerjaar 1 aan de orde zijn gekomen en stelt dat er allerlei rechte, ronde, hoekige, spiraalvormige, scherphoekige en stomphoekige lijnen getekend moeten worden om de handvaardigheid te ontwikkelen. Dit tekenen moet voorafgaan aan het leren schrijven. Uit zulke lijnen en vormen moet dan ontwikkeld worden wat nodig is voor het schrijven van de lettervormen.

Met vormtekenen gaf Rudolf Steiner ook een nieuwe impuls aan het tekenen in het algemeen. Hij stelde voor om kinderen in de onderbouw niet te vragen om uiterlijke dingen te tekenen – wat later zijn betekenis en educatieve waarde zou krijgen – maar om ze in plaats daarvan te laten beginnen met het tekenen van originele vormen, cirkels, driehoeken, hoeken, spiralen, etc. Hij maakte een duidelijk onderscheid tussen tekenen en schilderen. Bij schilderen gaat het erom zich volledig los te maken van het inkleuren van getekende contouren en vormen en te proberen de vormen, het representatieve, te laten ontstaan uit de ervaring van de kleurkwaliteiten, uit de oppervlakken van de geschilderde kleuren.

Als Rudolf Steiner erover spreekt dat de omtrekslijn in een schilderwerk onwaar is en energiek afstand neemt van het voortekenen, geeft hij daarentegen de lijn, als tot rust gekomen beweging, een nieuwe betekenis in het tekenen van zuivere vormen en bevrijdt het tekenen van zijn slaafse afhankelijkheid van de naturalistische reproductie van uiterlijke vormen – waarbij de mens een passieve imitator blijft. Het nieuwe in het tekenen ligt in het opnieuw, of beter gezegd mede-ervaren van de strekkingen en krommingen, de hoeken etc., zodat de vormen opnieuw ontstaan vanuit een innerlijk actief element, vanuit een innerlijk samengroeien met de vormen.

Rudolf Steiner wijst er altijd op dat men moet proberen het kind de vormen te laten ervaren, in hem een gevoel te wekken voor het gebogen zijn van cirkels, van ellipsen enzovoort. In de eerste methodisch-didactische lezing (21 augustus 1919) zegt hij zelfs dat je het kind er rustig op moet wijzen dat de hele persoon deelneemt aan de cirkelbeweging bij het tekenen, dat zelfs de ogen een cirkelbeweging uitvoeren.

Dit mede-ervaren, mede-voelen van de vormen, hun buigen, strekken, hun ritmes en bewegingen, is de nieuwe kunstzinnige ervaring die Rudolf Steiner bij de toeschouwer probeerde op te wekken toen hij over het eerste Goetheanumgebouw sprak.[GA 290, niet oproepbaar]  De architectonische vormen moesten niet alleen uiterlijk bekeken worden, de blik moest de vormen innerlijk plastisch en actief begrijpen.

Deze vormervaring is zowel de ziel van een nieuwe kunstzinnige ervaring als het orgaan van een levendigere perceptie van natuurlijke vormen. Hieruit kunnen we het verstrekkende belang van het tekenen van vormen afleiden.

In de lagere klassen moeten we vierkanten, cirkels, driehoeken enzovoort ook puur als tekeningen behandelen, “door wat dan geometrie wordt volledig binnen de tekening te houden.” “Wat dan als meetkunde wordt toegevoegd, waar we de relatie tussen de vormen zoeken, daar beginnen we pas rond het negende jaar mee”, zo vatte Rudolf Steiner zijn suggesties samen in de tiende lezing van de Methodisch Didactische Cursus  = Opvoedkunst (1 september 1919).

Pas op 14 augustus 1923 kwam Rudolf Steiner in Ilkley op het vormentekenen. Hij beschrijft het nu in samenhang met de werking van het etherische lichaam. Alle indrukken, legt hij uit, vooral de beeldende die het etherische lichaam heeft opgenomen terwijl het wakker is, hebben de neiging om verder te resoneren en zich te vervolmaken tijdens de slaap. We kunnen deze activiteit van het etherische lichaam ondersteunen door vormen te tekenen. Op deze manier hebben we een harmoniserend, stimulerend en versterkend effect op het etherisch lichaam en daarmee op de fysieke organisatie.

Figuur 1

Wat afgemaakt moet worden, geeft Niederhäuser hier als stippellijn. De verticale hulplijn zit op deze tekening vast aan de linker gegeven vorm. Dat is bij de tekening van Steiner bewust niet zo: de 2 lijnen vormen geen eenheid – de ene is slechts hulp:

Rudolf Steiner wijst in Ilkley voor het eerst op het principe van symmetrie met de eenvoudige tekening. De leraar tekent de linkerhelft op het bord en het kind wordt gevraagd de onvolmaakte helft aan te vullen. Rudolf Steiner zegt hierover: “Op deze manier krijgt het kind de innerlijke actieve drang om onvoltooide dingen te voltooien en zo een correct beeld van de werkelijkheid op zichzelf te vormen.” In de geest van deze basisuitspraken over de symmetrie-oefening is het nu aan de leerkracht om zulke eenvoudige oefeningen door inventief, flexibel denken te ontwikkelen tot meer gecompliceerde symmetrieën en deze een tijdje met de kinderen te oefenen.

In GA 307, de Illkleycursus, staat de tekening zoals hierboven, Nh. geeft hem zo:
(wat in wezen niets uitmaakt):

Figuur 2

Rudolf Steiner geeft nu een andere tekening (figuur 2) en legt uit dat men moet proberen om een innerlijke, ruimtelijke verbeelding van deze figuur bij het kind op te roepen. Rudolf Steiner hecht veel waarde aan deze ruimtelijke verbeelding. Naar aanleiding van deze figuur maakt hij de opmerking dat je in de meetkunde ook niet moet beginnen met het tekenen van driehoeken en dergelijke, omdat dit al te veel intellectualisme met zich meebrengt, maar dat je moet beginnen met zo’n levendige visualisatie van de ruimte als in bovenstaande oefening. Rudolf Steiner stelt nu voor om de uiterlijke om te vormen.Ongeveer zo: figuur 3. Hij vraagt: Hoe moet de binnenfiguur dienovereenkomstig worden gevarieerd? en vervolgt: “Probeer het kind duidelijk te maken dat als hij nu vasthoudt aan de binnenfiguur, hij, om de innerlijke symmetrie te laten ontstaan, een inkeping moet plaatsen binnen, waar buiten een uitstulping is, zodat, zoals hier in tekening 2, de eenvoudige lijn overeenkomt met de eenvoudige lijn, hier (figuur B) de uitstulping overeenkomt met een inkeping.” (zie figuur 4).

Figuur 3

Figuur 4

Hij verwijst naar de bovenstaande figuren als een schema. Hij laat dus alles open voor de vrijheid en inventiviteit van de docent om eenvoudigere oefeningen te ontwerpen als voorstadia of om verdere motieven te bedenken volgens het hierboven genoemde principe. Na de beschrijving van deze oefeningen vat Rudolf Steiner ze samen:
“Kortom, dit geeft het kind de mogelijkheid om asymmetrische symmetrieën te visualiseren. En op deze manier, tijdens het wakker zijn, bereidt men het etherische of vormkrachtenlichaam voor om tijdens de slaap verder te bewegen, en om in dit bewegen te vervolmaken wat het heeft doorgemaakt tijdens het wakker zijn. Dan wordt de mens, het kind, ’s morgens wakker in een innerlijk bezield en organisch bewegend lichaam van vormende krachten, en dat dus ook in het fysieke lichaam. Dit brengt een enorme vitaliteit in de mens.”

In dezelfde lezing introduceert Rudolf Steiner een nieuw thema met de volgende metamorfose: Een kalm uiterlijk motief houdt het evenwicht van het stoutmoedig naar buiten strevende innerlijke wezen: (figuur 5)

Figuur 5

Nu verandert hij de vorm en keert deze dynamisch om, niet wiskundig, maar artistiek:(inversie) de uiterlijke vorm divergeert nu hyperbolisch naar het onbepaalde, de innerlijke vorm concentreert zich als een zaadje als gevolg van de dynamiek van de omkering, en de harmonie wordt hersteld: figuur 6

Figuur 6

*

* De reproductie van de twee bovenstaande figuren is gebaseerd op het tekeningontwerp zoals ze door Carl Kemper zijn aangegeven. De reproductie van de stenograafschets (GA 307, laat ook andere interpretaties toe.
.

Op 15 augustus 1924 sprak Rudolf Steiner in Torquay opnieuw over vormentekenen. [GA 311]

De reflecterende vorm als nieuw element: het spiegelende wateroppervlak voor de acht- en negenjarigen met de volgende figuur: (figuur 7)

Figuur 7

en als uitbreiding geeft hij symmetrieoefeningen zonder symmetrieas:
(figuur 7a)


Figuur 7a

In Torquay geeft hij vervolgens nog een oefening vergelijkbaar met die in Illkley, maar veel eenvoudiger, voor achtjarige kinderen: (figuur 8)

Figuur 8

Opnieuw verandert hij de buitenkant van de vorm; hij tekent hem vierkant en geeft het kind de opdracht om zelf de overeenkomstige binnenvorm te vinden, zodat er een nieuwe harmonie ontstaat: (figuur 9)

Figuur 9

 “Op deze manier leert het kind een echt gevoel voor vorm, een gevoel voor harmonie, symmetrie en overeenkomst.” “Op deze manier kan het kind kennismaken met harmonieën die anders ook in de wereld voorkomen.”

We willen graag de opmerking toevoegen dat het, om methodologische redenen, raadzaam is voor kinderen om te beginnen met de eenvoudigere vorm van Torquay (figuur 8 en 9) aan het einde van de tweede en het begin van de derde klas en vervolgens de vormen van Ilkley  te ontwikkelen.(figuur 2, 4, 5 en 6)

We hebben ook gemerkt dat het makkelijker is voor de kinderen als je eerst de binnenvorm Y verandert en ze dan een geschikte omslag laat zoeken. Dit prikkelt hun verbeelding van vormen tot creatief vermogen. De meest uiteenlopende mogelijke oplossingen worden gevonden (figuur 10)

Figuur 10

en door deze zoektocht staan ze open voor de meest opwindende die de grootste tegenstellingen harmoniseert. (De laatste in de serie). De kinderen komen hier niet gemakkelijk toe en het veroorzaakt grote vreugdevolle verbazing.

Wie zich verdiept in deze aanwijzingen van Rudolf Steiner, krijgt bijna ondoorgrondelijke suggesties voor de stijl van een nieuwe vorm van opvoeding en onderwijs in het algemeen. De praktiserende leraar ervaart de vruchtbare kiemkracht, de progressieve, stimulerende, revitaliserende werking van deze vormen en tegenvormen eerst bij zichzelf. Hij merkt het heilzame effect tot in zijn ademhaling; verstarrende krampen worden opgeheven, zijn verbeelding en denken worden flexibel en zijn fantasie krijgt vleugels.

De aanwijzingen voor vormtekenen laat op indrukwekkende wijze zien hoe Rudolf Steiner zich geleidelijk een weg baant op dit gebied. Dit getuigt van de levendige ontwikkeling van de vrijeschoolpedagogie. Ook al zijn het idee en de menskundige grondslagen van deze opvoedingskunst het resultaat van een nieuwe inwijdingswetenschap, de praktische uitvoering en realisatie ervan wordt geheel door het leven gevormd. Rudolf Steiner had geen vast programma en systeem dat hij door de leraren gerealiseerd wilde zien. Stap voor stap ontwikkelde hij wat toen het leerplan werd met en vanuit de ontwikkeling en groei van de school, waarbij steeds nieuwe gezichtspunten naar voren kwamen die elkaar niet opheffen maar aanvullen.

Hij ontwikkelde het vormtekenen eerst in de context van de veelomvattende taak om temperamenten te harmoniseren en de scherpe kanten ervan om te vormen.

Hij gebruikte het vormtekenen ook om het tekenen van nieuwe prikkels te voorzien en het te bevrijden van zijn afhankelijkheid van de reproductie van de natuurlijke werkelijkheid. Hij opent een nieuwe creatieve vrijheid voor het tekenen: ontwerpen vanuit de kwalitatieve ervaring van de lijn, de rechte en gebogen lijnen en hun onmetelijke samenspel.

Vervolgens, na jaren van oefening, verdiept hij het tekenen van vormen en brengt het, als een middel om het intellect op te voeden via het element symmetrie, in intieme harmonie met de menskunde. Op deze manier wordt de vorming van het intellect geen driloefening en een spel met begrippen, maar ontstaat het intellectuele vermogen als een gevolg vanuit de hele mens. Hierover later.

*

Al deze schijnbaar eenvoudige oefeningen vinden hun oorsprong in de nieuwe impuls die Rudolf Steiner aan de kunst in het algemeen en aan de beeldhouwkunst in het bijzonder heeft gegeven. En vanuit deze nieuwe kunstimpuls, die in de vormen van het eerste Goetheanum geworteld is en volledig zichtbaar en voelbaar geworden is, moeten deze oefeningen ook door de leraar begrepen en geoefend worden. Zonder deze levende bron, zonder een nieuwe artistieke ervaring van vorm, zonder het idee van metamorfose en visualisatie, zou dit tekenen van vormen snel verstarren in een saai schematisme, zelfs met de beste didactiek.

De oefenende leraar vindt in het boek ‘Der Bau‘, uitgegeven door Carl Kempers vrienden , een schat aan suggesties en praktische hulp om de eerste Goetheanumbau in zichzelf tot leven te wekken. Kempers schetsen over de metamorfose van de kapitelen en het overbrengen ervan op de zegelvormen, om maar een motief te noemen, zijn van onschatbare waarde.

We willen deze innerlijke verbinding tussen sommige pedagogische vormen en de kunstimpuls van het Goetheanum visualiseren aan de hand van het voorbeeld van de zegels die Rudolf Steiner voor zijn vier mysteriedrama’s gaf. (Figuren 11 t/m 14)

Laten we proberen de vormentaal van deze zegels zo waar te nemen dat we ze niet intellectueel interpreteren, maar actief hun vormentaal volgen door ze eenvoudig na te tekenen, de vormbewegingen meebeleven.

Het nieuwe van de artistieke waarneming ligt in een dergelijke inspanning. Vervolgens beleven we een dynamiek in de opeenvolging van deze vier zegels: van een zekere rust met toch een bepaalde spanning, en eenvoud, wordt de vorm gecompliceerder, wordt weer eenvoudiger in de derde tot een zeer bezielde vorm en bereikt in de laatste een alomvattende, vervulde rust. Bovendien ervaren we als we tekenen een gedifferentieerd samenspel en interactie tussen de omcirkelende krachten en het centrum.

Laten we proberen de dynamiek van de binnen- en buitenkant van de eerste zegelvorm door ervaring te begrijpen. Als we een beetje spelen met het vormprincipe van de naar binnen gerichte actie

en de naar buiten gerichte straling

kunnen we gemakkelijk de volgende samenhang ervaren. (figuur 15.):

 

 

 

We komen nu bij de vorm die Rudolf Steiner in Ilkley gaf. Die bevat, op een eenvoudige manier, hetzelfde principe van spanning tussen binnen en buiten in een drie-eenheid, die in de eerste zegelvorm wordt geïntensiveerd in een zevenvoudig effect.

Laten we nu kijken naar een detail van de vormen van Torquay en Ilkley (fig. 16): daar ervaren we de grootste spanning tussen innerlijke vorm en uiterlijke omhulling.

 

 

Fig. 16

Dit dynamische spanningsprincipe (figuur 17) is ook terug te vinden als karakteristiek ontwerpelement in het tweede (figuren 12 en 18).

 

 

 

 

 

 

 

Figuur 12: gegeven bij ‘Die Prüfung der Seele’
GA 14/157
Vertaald/158

 

 

 

 

 

|
Figuur 18

In de spiraal wordt de intensivering van de tegenstelling opgeheven of is de bron van de vormende kracht.

Als je de innerlijke kunstzinnige samenhang ziet tussen de zegelvormen die Rudolf Steiner voor de mysteriedrama’s gaf en de pedagogische vormen die jaren later werden gegeven, wordt de gemeenschappelijke oorsprong in de Goetheaanse artistieke impuls duidelijk. Dit laat zien hoe zelfs een ogenschijnlijk detail van de vrijeschoolpedagogie geworteld is in het geheel van de antroposofie dat zonder deze achtergrond niet creatief vormgegeven kan worden. Het is belangrijk dat de leerkracht dit weet en ervaart. Voor de kinderen is het voldoende als ze de pedagogische vormen van Ilkley en Torquay ervaren door te oefenen met tekenen. Hiervan uitgaand kan men proberen soortgelijke spanningsmotieven te creëren. Maar we denken dat het helemaal verkeerd zou zijn om te proberen de zegels met de kinderen te tekenen, hoe mooi ze ook zijn. Net als de zegels op de zuilkapitelen van het eerste Goetheanumgebouw maken ze deel uit van het ontwikkelprogramma van de leraar, waarmee hij zijn vormverbeelding verlevendigt.

Nog een paar voorbeelden van de genoemde planetenzegels (die verder niet worden besproken):

 

 

 

 

 

 

Figuur 11: gegeven bij ‘Die Porte der Einweihung’
GA 14/9
Vertaald/17

 

 

 

 

 

 

 

Figuur 13: gegeven bij ‘Der Hüter der Schwelle
GA 14/281
Vertaald

 

 

 

 

 

Figuur 14: gegeven bij ‘Der Seelen erwachen’
GA 14/405
Vertaald

*Zo was het in de tijd van Niederhäuser. Door het werk van Kutzli deden in de jaren 1970 ook de vlechtvormen hun intrede. Deze kunnen in moeilijkheidsgraad zodanig verschillen, dat oefenen daarvan in klas 6 en hoger ook uiterst zinvol is.

Deze leerstof wordt ook behandeld in ‘Formenzeichnen’ (Menschenkunde und Erziehung)

Deel 2 deel 3 deel 4 deel 5

Vormtekenen: alle artikelen

Rudolf Steiner over vormtekenen: alle artikelen

Algemene menskunde: alle artikelen

Rudolf Steiner: alle artikelen op deze blog

Menskunde en pedagogie: alle artikelen

Vrijeschool in beeld: alle beelden

.

3446-3244

.

.

.

.

Een reactie plaatsen

Geplaatst in vormtekenen

Getagged , , , , ,

VRIJESCHOOL – Vormtekenen (2-3/4)

Geplaatst op 22 juni 2020| Een reactie plaatsen

.

FORMENZEICHNEN                                            VORMTEKENEN

Zie de inleiding

Hoofdstuk 3/4

Margrit Jünemann†:

DE LEERPLANAANWIJZINGEN VAN RUDOLF STEINER VOOR HET VAK VORMTEKENEN MET VOORBEELDEN UIT DE ONDERWIJSPRAKTIJK

(Dit is geen letterlijke vertaling. De opmerkingen, verwijzingen e.d. in blauw zijn van Pieter HA Witvliet)

Symmetrie

Tekeningen die spontaan ontstaan bv. naar aanleiding van een verhaal of een gebeurtenis, laten veel van de aard van het kind zien. De vormen spreken een taal. Hoe wordt de ruimte gebruikt en zijn de vormkrachten vrij geworden en nog meer, dat alles laat iets zien van de ontwikkelingsfase waarin het kind zit.
Zo tegen het achtste jaar komen daar de symmetrische elementen en vormgeving bij.

Soms zie je ze al eerder: deze kleuters hebben de meiboom aandachtig waargenomen en blijken in staat tot enige symmetrie.
De tekeningen laten ook nog ‘oervormen’ zien. Zie daarvoor kindertekeningen. [1]   [2]   [3]  [4]  [5]

Wel een heel mooi voorbeeld van een ouder kind:

Jünemann:
Bij symmetrie heb je ‘een midden’ nodig.
Het kleine kind leert dit voor het eerst vinden wanneer het gaat staan en zijn evenwicht moet zien te bewaren. Bij elke (eerste) stap moet dat ook bewaard blijven en vooral in het begin is dat nog een hele opgave. Maar, zoals we weten, lukt het steeds beter de zwaarte te overwinnen, in evenwicht te blijven en vooruit te komen.
Daarna komt er bij de meeste kinderen een sterke behoefte om te balanceren: tijdens het spelen, bij het wandelen, overal wordt geprobeerd zolang mogelijk op de rand, balk of het muurtje te kunnen blijven.
Deze ‘symmetriekrachten’ zijn dus eerst werkzaam bij het doen functioneren van het fysieke lichaam, vooral vóór de tandenwisseling, maar ook in dit evenwicht te bewaren, tevens in de opbouw, de architectonische bouw.
Nu lijkt het erop dat er een soort bewustzijn – een zielenfunctie! begint te ontstaan voor deze symmetrie. Een gevoel ontstaat voor ‘wat bij elkaar hoort, voor het symmetrische’ [10]

Steiner wees op de symmetrie voor het eerst in Ilkley [ 11]* Ook bij vormtekenen – hij noemt dit een deel van het beeldend leren – moet het ‘innerlijk’ kijken zo behandeld worden, dat het denken zich daaraan kan ontwikkelen, zonder intellectualistisch te worden.

Hij tekende op het bord de linkerhelft van een figuur, een simpele boog. Daarnaast een lijn en rechts daarvan een stuk van de symmetrie.
Deze tekening staat niet in de Ilkley-cursus, maar in GA  311 (Bern)

In GA 307 (Ilkley) staat deze:

In kleur:

Naar deze tekening laat Steiner de kinderen goed kijken en dan komt eruit dat deze niet ‘af’ is. Zie de volledige tekst daarvan – op deze blog vertaald.

Dat iets ‘niet af’ is, is het belangrijkste. Want het ‘af-zijn’ moet voorgesteld worden. Dat moet uit het kind komen.
Dit soort oefeningen waarvan je er veel met verschillende vormen kan geven, weer afgewisseld met andere, wekken in het kind een voorstellingsgevoel op om dingen ‘dienovereenkomstig’ vorm te geven.  Dat is ‘op weg’ naar een juiste voorstelling van een werkelijkheid.

Fysiek gesproken gebeurt ‘het afmaken’ door het etherlijf. Als we een wond hebben, ‘weten’ de levenskrachten deze weer in de oorspronkelijke vorm, de eenheid’ te brengen; ze herstellen wat on-af is. Hier ligt een samenhang tussen de scheppende voorstellingskrachten en het etherlijf in het denken.

Wanneer je de voorbeelden die Steiner geeft op het gebied van de symmetrie, bestudeert, zie je de axiale symmetrie, het spiegelen en de a-symmetrische symmetrie. Bij hem zijn het allemaal ronde vormen, met of zonder lussen.
Bij allemaal gaat het om het evenwicht in het voorstellen, links – rechts, boven- beneden; binnen-buiten. Tegelijkertijd moet er enige vaart in zitten, een bewegingsstroom, iets dynamisch.

Het tekenen van symmetrie-oefeningen vinden tweedeklassers heel fijn om te doen. Natuurlijk moet je eenvoudig beginnen. Het schatten van het midden is ook al een goede opgave voor het evenwichtsgevoel. Het is natuurlijk het mooist als de kinderen dat precies kunnen ‘zien’. ‘Zet in het midden een klein stipje’. Ter controle kun je het blad laten vouwen en dan zien hoe ver het stipje van het midden staat. Je kan op het tekenvel ook gelijktijdig en gelijkmatig je linker- en rechterhand naar het midden toe bewegen. Waar ze elkaar raken is het midden.
Je kan de verticaal over de vouwlijn trekken, maar later moeten de kinderen zonder vouwlijn of ‘uitgerekend’ dat midden kunnen bepalen. Trek je die middenlijn, heb je de neiging naar je potlood te blijven kijken, maar eigenlijk moet je naar je eindpunt kijken en daar in één zekere beweging naar toe gaan.

Als dan de linkerhelft van de tekening staat, kan de rechter precies hetzelfde maar dan gespiegeld aan de rechterkant komen, met evenveel afstand tot de verticaal.

Wanneer de linkerhelft gegeven is, moet de rechterhelft worden gevonden.
Om het principe duidelijk te maken, kan je zo te werk gaan als Steiner deed. Maar als de werkwijze duidelijk is, kun je – met het oog op ‘er moet iets worden voorgesteld’- ook de linker vorm voor de kinderen in de lucht tekenen. Dan is er nog geen concrete lijn, alleen een beweging. 
Als je deze linker lijn in de lucht voortekent, moet je er rekening mee houden dat de kinderen goed naar je (moeten) kijken. Wanneer de opdracht luidt deze linker vorm eerst met de linkerarm in de lucht te bewegen – moet jij als leerkracht – met je gezicht naar de kinderen staand – deze vorm met je rechterhand voordoen. Veel kinderen zullen namelijk – als jij het met je linkerarm voordoet – je spiegelen: dan doen zij het met hun rechter! Dat kun je voorkomen door met je rug naar de kinderen te gaan staan: dan kan jij ook je linkerarm gebruiken. Een nadeel is dat je dan niet ziet hoe ieder kind het doet. 
Wanneer die linker vorm goed geoefend is, d.w.z. de kinderen ‘kennen’ hem en kunnen hem maken zonder dat jij meedoet – je kan dat controleren door het een aantal kinderen op het bord te laten doen – moet het spiegelbeeld in de lucht komen. Eerst kan de linkerarm nog helpen en doe je de vormen met beide armen in de lucht. Net zolang tot de rechterarm deze vorm alleen kan maken. 
Een vraag zou nog kunnen zijn hoe het met de linkshandige kinderen moet. M.i. kunnen die tot zover alles gewoon meedoen. 
Wanneer dan de rechterarm de vorm kent, kan je deze nu met de wijsvinger bewuster nog, in de lucht laten tekenen en deze dan laten maken – nog steeds met de vinger – groot op het tafelblad.
Op dat ogenblik kunnen de linkshandige kinderen hun ‘schrijfhand’ gaan gebruiken.
Dan komt het papier en het (dikke) potlood of krijtje. 
(Opmerkingen over het materiaal vind je hier) 
Over ‘zitten of staan’ zijn hier gezichtspunten gegeven.

Nu kunnen de kinderen hun opdracht op papier uitvoeren, waarbij dus eerst de denkbeeldige middenlijn wordt bepaald, dan de linker vorm wordt gemaakt en dan de rechter – de eigenlijke opdracht.
Veel oefenen, corrigeren over- of door de eerst opgezette vorm heen. Net zolang tot het gelukt is, m.a.w. tot het kind het kan.

Het ‘hoofdmotief’ uit de 1e klas kan ook hier als uitgangspunt worden genomen.

Hier is de gele middenlijn nog duidelijk als hulp aanwezig.
In het vervolg van de oefeningen moet de hulplijn steeds onzichtbaarder worden. 

In GA 311 – op deze blog vertaald – geeft Steiner een paar symmetrie-oefeningen:

zie voor de bijbehorende tekst: Steiner over vormtekenen

In bovenstaande tekening is geen sprake van één vorm: dit blijven twee losse.

Wanneer de vormen echter ‘naar elkaar kijken’ kunnen ze wél aan elkaar vast getekend worden. En dan ontstaat er een gesloten vorm, waarvan het vlak ineens de aandacht vraagt. 

Hier een vorm waarbij de middellijn ‘gedacht’ is:

Jünemann:
De ervaring leert steeds weer dat de moeilijkheid voor de leerling ligt in het even ver afstand houden van de middellijn aan beide zijden. Dat moet het kind gaan zien en in de tekening waaraan het bezig is, zo proberen te corrigeren dat het goed is. Wanneer een kind het niet ziet, kun je de binnenvlakken laten kleuren en dan valt aan het kleurvlak het grote(re) verschil op.
Het wezenlijke van de symmetrie-oefeningen is dat het kind leert een harmonieuze vorm te tekenen.

Jünemann verder:
In de loop van het tweede schooljaar, wanneer je met de kinderen een tijd de links-rechtssymmetrie hebt geoefend, kan je naar de spiegeloefeningen overgaan. Die brengen je in een andere beleving van de ruimte. Eerst komt er bewustzijn voor boven en onder, wanneer je de horizontaal trekt. De eenvoudige lijn boven die gespiegeld moet worden, teken je eerst vrij zwevend boven de horizontaal, dan eronder. Uiteraard zijn er weer veel mogelijkheden.
Het is aan te raden om gecompliceerde vormen pas aan het eind van de tweede klas te maken. Die vragen de vaardigheid om met afstand het geheel te kunnen overzien. Jongere kinderen doen de ondervorm vaak hetzelfde als de bovenvorm, of de ondervorm wordt veel te klein, zodat er geen echte symmetrie is.

Combinaties van links/rechts met boven/onder zijn een goede voorbereiding voor de oefeningen die van een middelpunt uitgaan.

Wanneer je bv. zoiets wil laten tekenen:

en je geeft de leerlingen alleen de linkervorm, moeten ze deze naar rechts, naar boven en beneden afmaken. Ook daarin natuurlijk weer allerlei variaties.

De voorbereiding van zo’n oefening was (enige tijd terug) bv. deze:

en die waarbij de blauwe lijn horizontaal loopt.

Het kan ook ‘schuin’.

Bij deze oefeningen gaf Steiner een aanwijzing hoe je bij de kinderen daarmee een gevoel voor stijl ontwikkelt. [12**]

Het gaat erom dat je bewust leert kijken naar karakteristieke vormelementen. In een figuur met vier bogen tekende hij een lijn die in de tegengestelde richting naar boven opengaat, net als de boog. Daarbij dan een even grote vorm met rechte lijnen. In deze moeten de leerlingen nu een vorm vinden die daarbij past.

Het probleem bij deze oefeningen is dat het niet zo makkelijk is ze zelf te bedenken, omdat je dan zeker moet zijn dat de ‘tegenvorm’ kunstzinnig gezien. ‘klopt’ – en wie bepaalt dat.
(Ik denk dat dit de reden is waarom je er in allerlei boeken, artikelen, zo weinig voorbeelden van ziet)
Ik heb wel altijd aan de kinderen gevraagd of ze er zelf twee zouden kunnen ‘bedenken’.

Jünemann:
Met deze oefening is een typerend voorbeeld gegeven van hoe uit een subjectieve omgang met de vorm een objectievere kan ontstaan.
Je moet hier wel de leeftijd in acht nemen waarin het kind zich bevindt. Dat is tegen het tiende jaar. En hierin verandert de houding van het kind t.o. de wereld. De vanzelfsprekende verbinding hiermee gaat verloren. Er ontstaat een kritischer houding, die tegelijkertijd vaak onzekerheid meebrengt. De oefeningen die nu gegeven worden proberen vanuit een zekerheid: de gegeven vorm, te zoeken naar harmonie met een nog ongewisse vorm. Kan er weer eenheid ontstaan?
Hierop gebaseerd zou je ook alleen maar de binnenvorm kunnen geven, recht of rond. Deze vorm die geen omhulling heeft, moet die wél krijgen en hoe vind je het antwoord daarop. Het moet eigenlijk om kleine aanpassingen gaan – geen overdaad – een soort ‘precieze kunstzin’, een ‘exact vormgevoel’ – voor zover dat bestaat.

Jünemann zegt over de verticaal en de horizontaal, dat als deze in een vorm gebruikt worden, de vorm een enigszins statisch karakter heeft; wanneer de scheidslijn een diagonaal is, veel minder. Vanuit het punt werkt het vrijer de ruimte in. Ze merkt op dat Steiner veel van de diagonaal uitging.

A-symmetrische symmetrie

Een enigszins paradoxale naam, maar het gaat om vormtekeningen waarin wel een ‘soort van middenas’ is te herkennen, maar waarbij de vormen zich niet direct aan weerszijden van de as spiegelen. Toch is er iets van spiegeling in te herkennen, maar deze ‘dwingt’ niet meer: nu gaat het veel meer om de vorm, de buitenkant en de daar bijhorende binnenkant, zoiets als we hierboven al zagen.
Deze oefeningen zijn er vooral om het stijlgevoel van de kinderen te ontwikkelen.

In GA 307 geeft Steiner deze vorm:

die dan zo moet worden:

Tenminste, dat zou je op grond van de tekening in de voordracht – die niet erg duidelijk is – verwachten. Als je ‘logisch’ kijkt, zou de buiteninstulping boven de blauwe instulping juist niet naar binnen moeten gaan, maar naar buiten.

Jünemann tekent deze dan ook zo:

Dat is meer in overeenstemming het het woord ‘Entsprechung’: wel een tegenstelling, maar toch bij elkaar horend.

Ook hier is de moeilijkheid voor de leerkracht: hoe vindt hij de geschikte vormen en hoe ‘juist’ is de tegenstelling die toch een symmetrie moet zijn.

Eigenlijk wordt er van de leerkracht een sterk gevoel voor metamorfose gevraagd. De een zal dat meer van nature hebben, dan de andere.
Steiner hanteert de metamorfose in bv. de grafische ontwerpen van logo’s maar vooral bij de zgn. ‘planetenzegels’.

Jupiter

Rudolf Kutzli heeft in zijn ‘Formenzeichnen‘ een methode ontwikkeld om deze planetenzegels te leren tekenen en daarmee te leren ‘zien’. Daardoor kan je je gevoel voor metamorfose en wat aan veranderde vormen toch met andere vormen een eenheid vormt, ontwikkelen.

Als je er a-kunstzinnig naar kijkt, dus bv. wat analyserend, kan je wel ‘de beweging’ ‘snappen’, deze ‘zien’, maar dat is weer het bekende ‘na-denken’ van wat al gedacht is, gezien is, terwijl bij het ontwerpen van dergelijke vormen een ‘vooruit-zien’ van je gevraagd wordt.

Eerst hebben we deze vorm:

die aan de bovenkant wat wordt ‘ingedeukt’:

wat in de ene vorm zit, wordt in de andere vorm ook ingedeukt, maar tegenovergesteld:

Jünemann:
Hier gaat het er niet om bij de buitenvorm die ook weer het eerst getekend moet worden, een dienovereenkomstige binnenvorm te vinden om door het kloppen van de lijntaal op het stijlgevoel van het kind te werken, veel meer komen drie van buiten komende rondbogen samen en raken elkaar aan. Vanuit het middenpunt ontvouwt zich een soort smal klaverblad. De verandering die in de volgende tekening moet komen, begint bij de buitenbogen. Die worden beweeglijker en er ontstaan in/uitstulpingen. De opgave is op ook de binnenvorm dienovereenkomstig te veranderen, zodat er evenwicht ontstaat, d.w.z. tegenover een uitstulping staat een instulping. De totaalfiguur laat geen symmetrie zien, het is een drieheid. De symmetrie is er wel, maar daar waar een uitstulping en een instulping bij elkaar horen.
Dat noemt Steiner de a-symmetrische symmetrie.

Drie zaadachtige figuurtjes (de grotere) zijn gegroepeerd om een vrij midden, met daarin naar buiten strevend, ook een soort zaadjes. De verandering in de tweede tekening begint met het groter, wijder worden van de buitenvormen. Dat roept voor het midden een tegenbeweging op. De eerst nog vrij liggende ‘zaadjes’ ballen zich samen tot eenheid, vormen een vast middenpunt. Dat er bij deze voorbeelden alleen maar ronde lijnen zijn, is begrijpelijk. Het zich verwijden en samentrekken vereist dit, want de verandering speelt zich helemaal af in het vlak van de beweging. Rechte lijnen die zich tot hoeken en zijden samenvoegen, brengen meer het architectonische van een vorm tot uitdrukking.
Omdat het om voorbeelden gaat die het geometrische tekenen voorbereiden [13], helpen ze de leerling een beweeglijk voorstellen te ontwikkelen en daarbij wordt een intiemer waarnemen beoefend.

Dat zijn wel de moeilijkste opgaven. De zich naar drie kanten openende vorm gaat uit van een middenpunt. De indeling moet wakker, met gevoel voor de juiste afstand worden gemaakt.
Hier kan de leerkracht nog helpen, wanneer hij eerst met drie eenvoudige lijnen die vanuit een middelpunt lopen, laten zien wat voor vlakken er ontstaan, ook wanneer de lijnen te ver of te dichtbij van elkaar staan. Als dat goed begrepen is, begin je de bogen te tekenen vanuit het midden. De leerling staat a.h.w. in het midden en probeert voorzichtig wikkend en wegend hoe de lijn moet lopen, spontaan beginnen is niet mogelijk.

Vorm en kleur

Ten slotte nog een woord over de vraag naar een kleurige voorstelling van de tekeningen.
Het gaat bij het vormtekenen in eerste instantie om de scholing van het vormgevoel. In de ‘Pedagogische jeugdcursus’ maakt Steiner erop attent dat er in het kind naast het vormgevoel ook kleurbeleven gewekt moet worden [14] Hij maakt dat met verschillende cirkeloefeningen duidelijk en tekent in twee groene cirkels drie rode die dan ook in omgekeerde volgorde getekend moeten worden. Ook op het bord verdient het kleurkrijt voorrang boven het witte krijt, want dat spreekt meer tot het gevoel van het kind.
Het is ook mogelijk door de kleur het karakter van een lijn of een vorm nog te benadrukken. De actieve kleuren zoals rood en oranje zijn meer geschikt voor het dynamische, blauw en groen daarentegen ondersteunen de statisch-rustende vormen. Vanzelfsprekend laat je het ook steeds weer aan het kind over om de ene of de andere kleur te kiezen.
Bij het samen naar de vormen kijken is er dan wel gelegenheid om erop te wijzen waar het gelukt is, kleur en vorm in harmonie te brengen.
.
[10] Steiner GA 307 voordracht 10 blz. 161 (foutieve vermelding bij voetnoten: GA 309)
Vertaald
*[11] Steiner, GA 311 voordracht 4, blz. 73.
Op deze blog vertaald
**[12] Steiner GA 307 en niet zoals vermeld in de voetnoot GA 303
[13] Steiner GA 307 zie boven [10] – foutief vermeld in voetnoot GA 309
[14] Steiner GA 217 voordracht 10 blz. 146
Niet vertaald
.
Jünemann: over ‘de rechte‘

Junemann: over de ronde”

Het boek ‘Formenzeichnen‘: inhoud   (vertaald)

Vormtekenen: alle artikelen

Menskunde en pedagogie: alle artikelen

Vrijeschool in beeld: alle beelden

.

2267-2129

.

.

.

.

 

Een reactie plaatsen

Geplaatst in vormtekenen

Getagged , ,