.
Alexander Strakosch:
‘Geometrie durch übende Anschauung’
Blz. 33 t/m 35
De verhoudingen van de onderscheiden lijn en de twaalfpuntscirkel in het geval van een onregelmatige driehoek
Dit hoofdstuk staat niet los van 4-7 en begint met de 3 bijzondere punten in een driehoek: hoogtepunt, middelpunt van de omgeschreven cirkel.
Als deze drie onderscheidende punten bepaald zijn, blijkt dat ze altijd op één rechte lijn liggen waarvan de positie en lengte variëren afhankelijk van de vorm van de driehoek. De afstand tussen het snijpunt van de hoogtelijnen en het snijpunt van de loodlijnen vanuit het snijpunt van de medianen is echter altijd evenredig met 2/3 tot 1/3.
Deze lijn wordt de lijn van Euler genoemd, naar de ontdekker ervan, de Zwitserse wiskundige Leonhard Euler (1707-1783). Het halveringspunt is het middelpunt van de cirkel van de twaalf punten. De relatie tussen deze punten blijft namelijk in elke willekeurige driehoek bestaan, waarbij de drie hoogten elkaar in één punt snijden, evenals de zijdehalveringen onderling en ook de middellijnen. — Het feit dat ze alle negen op een cirkel liggen, werd voor het eerst ontdekt door Karl Wilhelm Feuerbach, Erlangen (1800-1834), met betrekking tot de voetpunten van de hoogtes, de middenpunten van de zijden en de halveringspunten van de bovenste hoogte-segmenten, en daarom wordt de cirkel meestal de cirkel van Feuerbach of de negenpuntscirkel genoemd. De laatst genoemde drie punten (blad VI, tekening 11) werden ontdekt door de Zwitserse wiskundige Jakob Steiner (1796-1863), voordat hij de cirkel van Feuerbach kende; hij heeft ook voor alle twaalf punten het algemene bewijs geleverd.
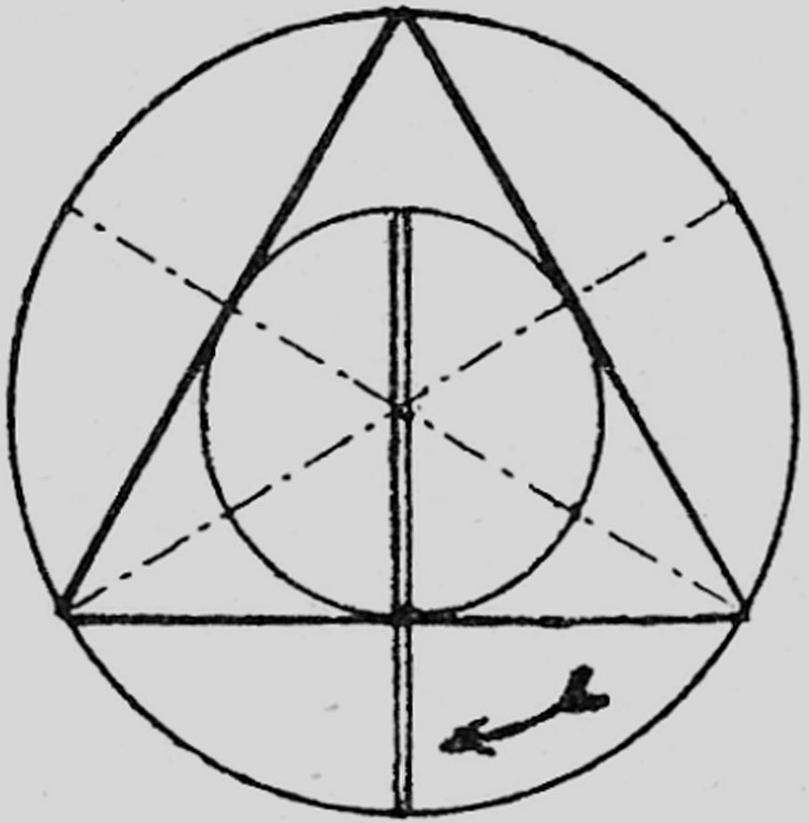
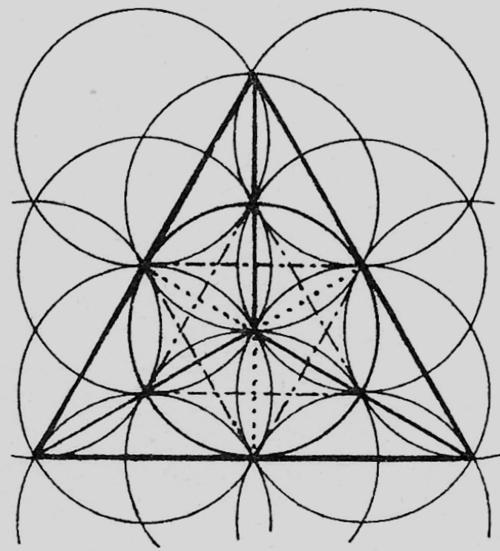
Bij het bekijken van de gelijkzijdige driehoek en het hexagram binnen de ‘bloem’ komt de wetmatigheid van de twaalfheid, gegroepeerd rond een middelpunt, naar voren, en wel in verband met de verhouding 2/3 : 1/3. Aan het feit van de twaalfpuntige cirkel kan men zien dat deze – weliswaar in bewegelijke vorm – toch altijd behouden blijft. Het blijkt een werkelijk algemene wetmatigheid van het vlak. Men begrijpt dat van oudsher het getal ‘twaalf’ het getal van de ruimte werd genoemd en dat er in het oude Babylon en Egypte naast de aanduidingen voor de opeenvolgende gehele getallen ook een speciaal teken voor de waarde 2/3 bestond.
De vraag blijft wat er gebeurt met de twee driehoeken die bij de gelijkzijdige driehoek het hexagram vormen dat in de binnenste cirkel is ingeschreven.
De zijden van deze driehoeken zijn hier paarsgewijs evenwijdig aan de zijden van de hoofddriehoek. Als de boven elkaar liggende eindpunten van twee van deze evenwijdigen met elkaar worden verbonden, ontstaat er een rechthoek, in totaal dus drie identieke rechthoeken.
In beide driehoeken valt het snijpunt van de zijdehelften samen met dat van de zijdehelften van de hoofddriehoek, dat in dit geval ook het middelpunt van de binnencirkel is.
Bij een ongelijkzijdige driehoek is er ook een binnencirkel. Het middelpunt ervan ligt echter in het snijpunt van de hoekhelften en heeft niets te maken met de punten die op de rechte lijnen van Euler liggen. Men kan zeggen: bij een gelijkzijdige driehoek valt de binnencirkel samen met de cirkel van de twaalf punten (VI, 8).
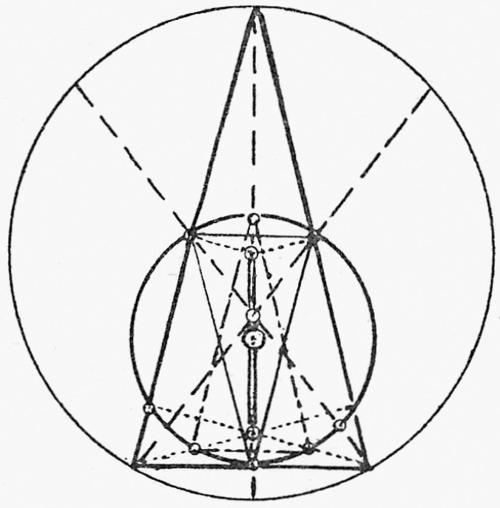
Maar bij een gelijkbenige driehoek is dit al niet het geval (VIII, 7):
Bij een ongelijkzijdige driehoek ontstaan opnieuw de ingeschreven driehoeken: de ene door de halveringspunten van de zijden van de hoofddriehoek met elkaar te verbinden, de andere door de middelpunten van de bovenste hoogte-segmenten met elkaar te verbinden. Deze zes punten liggen allemaal op de cirkel van de twaalf punten
zie blad VIII, tekening 8
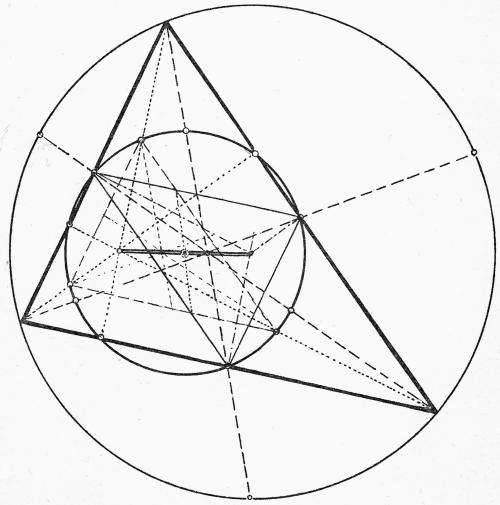
en IX, tekening 1:
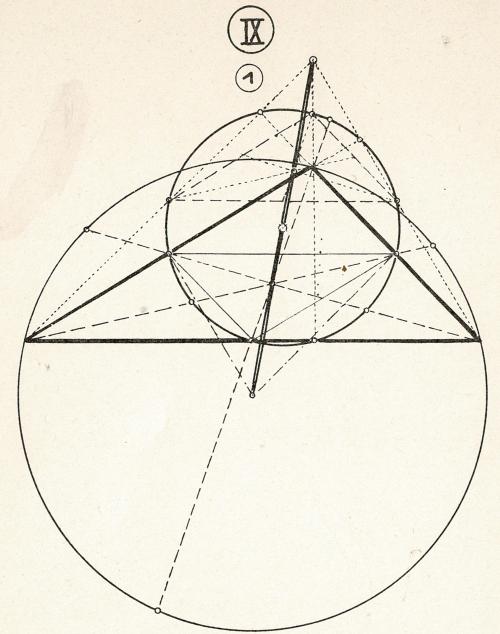
De eerste heeft met de hoofddriehoek de zijdehelften en daarmee ook hun snijpunt gemeen; de zijdehelften van de tweede snijden elkaar alle drie in een punt op de rechte van Euler, dat het traject tussen het hoogte-snijpunt en het snijpunt van de zijdehelften van de hoofddriehoek halveert, dus de hele rechte van Euler in drieën deelt, resp. in tegengestelde richting in de verhouding 2/3 deelt.
Er ontstaan ook weer drie rechthoeken, maar bij elk daarvan is de grootteverhouding van de zijdenparen verschillend, terwijl die bij de gelijkzijdige driehoek hetzelfde was. Ze zijn niet getekend in blad VIII en IX. Bij het oefenen met tekenen kunnen ze worden toegevoegd, bij voorkeur in kleur.
Het kan echter ook voorkomen dat bij een ongelijkzijdige driehoek de hoogten en de middellijnen elkaar snijden in punten die buiten het door de zijden omsloten driehoekige vlak liggen. De (IX, 1) verbindingslijnen van de drie hoekpunten met het hoogte-snijpunt liggen bij twee zijden buiten het driehoekige vlak; zij worden hier door de cirkel van twaalf punten gehalveerd. Bij de ene hoogte, die gedeeltelijk door het driehoekige oppervlak loopt, wordt het stuk tussen het hoogte-snijpunt en de ene hoek in aanmerking genomen, dat buiten de driehoek ligt.
De binnenste driehoeken snijden elkaar in een dergelijk geval niet, ze zijn uit elkaar geduwd, maar verder blijft alles zoals zojuist getoond.
Er zij nog op gewezen dat ook hier in de rechthoeken uit willekeurige aannames altijd rechte hoeken ontstaan, zoals ook het geval was in het cirkelveld bij de richtingsverhouding tussen het grote en het kleine blad. De rechte hoek blijkt dus ook hier een uitdrukking te zijn van een algemene ruimtelijke wetmatigheid.
Voordat we ons op de volgende beschouwingen richten, willen we nog even de volgende opgave behandelen:
Een gelijkzijdige driehoek tekenen wanneer de hoogte ervan bekend is.
De oplossing van deze opgave volgt uit de ‘bloem’ (tekening VIII, 5),
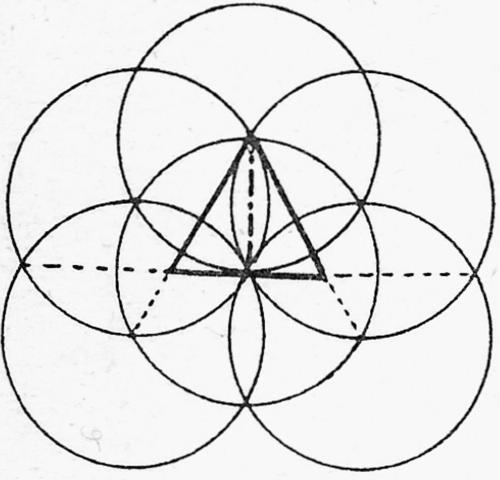
die zo wordt getekend dat de gegeven hoogte de straal van alle cirkels vormt. Vervolgens kan men snel de richting van de twee zijden van de gezochte driehoek vinden, die vanuit de top uitgaan. Nu moeten alleen nog de lengtes worden bepaald. De hoogte is de middellijn van een klein “blad”, de middellijn van de twee aangrenzende “bladeren” staat loodrecht daarop en bevat de gezochte basislijn van de driehoek; daarop snijden de middellijnen van de twee grote bladen de juiste lengte af.
Men kan echter ook te werk gaan volgens blad VIII, tekening 6,
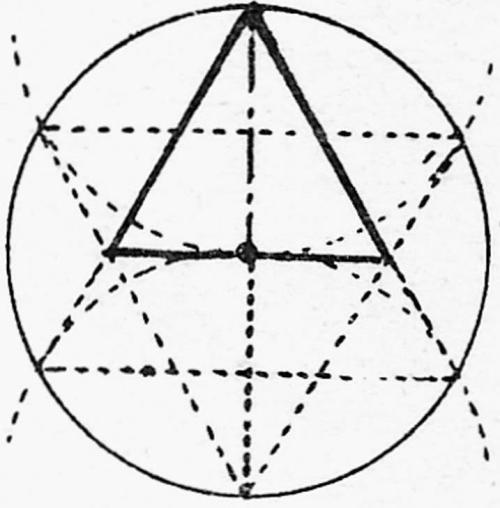
door rond elk van de twee eindpunten van de hoogte een cirkel te tekenen die door het andere eindpunt gaat. Vervolgens verlengt men de hoogte naar beneden tot het snijpunt met een van de cirkels. Rond dit punt tekent men een cirkel met dezelfde straal. Op deze manier ontstaan de zes hoekpunten van een hexagram en daaruit, zoals te zien is op de tekening, de lengte van de zijde van de driehoek.
.
Meetkunde: alle artikelen
Algemene menskunde: alle artikelen
Rudolf Steiner: alle artikelen op deze blog
Menskunde en pedagogie: alle artikelen
VRIJESCHOOL in beeld: 6e klas meetkunde
.
3504-3292
.
.
.
.
