.
De Zwitserse vrijeschoolleerkracht Hans Rudolf Niederhäuser schreef in de jaren o.a. 1970 artikelen over vormtekenen in het pedagogisch vrijeschooltijdschrift ‘De mensenschool’.
Ze werden in een boekje samengebracht.
In het laatste hoofdstuk geeft hij nog een kleine samenvatting en neemt daarna een artikel op van Hermann Koepke die een bepaalde visie heeft op de m.n. symmetrieoefeningen en de vorming van het gebit.
Belangrijke menskundige toevoeging
In een vorig deel is erop gewezen dat er drie niveaus moeten worden onderscheiden en in aanmerking genomen in de methodologische structuur van het vormtekenen:
De vormen van de 1e klas moeten gebaseerd zijn op de eenvoudige verticale symmetrieas.
In de 2e klas moet de horizontale symmetrieas geïntroduceerd worden als een nieuwe en dan overgaan op axiale symmetrie.
In een derde stap (rond de leeftijd van 8 of 9 jaar) kunnen vrije vormen worden overwogen die de nadruk leggen op binnen-buiten, centrum en omtrek; asymmetrische symmetrieën, zoals Rudolf Steiner ze noemt.
Hermann Koepke, leraar aan de Rudolf Steiner School Birseck in Dornach, heeft nu aangetoond dat deze drie stadia precies overeenkomen met het proces van tandvorming en de symmetrie of asymmetrie ervan weerspiegelen.
Over de vormen van symmetrie
Kinderen houden op een speciale manier van vormen tekenen. Zodra de schriften en kleurdozen op tafel liggen, breidt zich een heerlijke werksfeer uit met een gevoel van welbehagen.
Ik vind een schrift geen goed idee. Vellen papier, waarop naar hartenlust geoefend kan worden, opnieuw en opnieuw. Een schrift vraagt toch om ‘iets moois’ en dat is nu net wat de vormtekening pas op het allerlaatst van het oefenproces mag (niet moet) zijn. Natuurlijk, als het kind de vorm goed beheerst, er eigenlijk niets meer aan te oefenen heeft, is een neerslag in een schrift zeker een mooi afronding.
Het is alsof je een reis naar het dwergenrijk kunt maken, waar het werk wordt gedaan en gevormd in de organische, levende wereld.
Koepke refereert hier waarschijnlijk (als kenner?) aan de elementairwereld.
Dan valt je nog iets op, namelijk dat de ‘dwergen’ in de tweede klas veel open plaatsen tussen hun tanden hebben. Ze werken dus ook ijverig aan de vorm.
De vorming van tanden op deze leeftijd volgt de wet van ‘symmetrie’, zowel rechts-links als boven-beneden. Werkt het kind aan de symmetrievormen?
Als het kind aan de symmetrieoefeningen werkt, doet het dat met dezelfde vormende krachten die optreden bij tandvorming.
Voor de leerkracht is het niet vreemd als moeilijkheden met symmetrische vormen hand in hand kunnen gaan met een problematische stand van de tanden, net zoals aan de andere kant de hulp bij het tekenen van vormen de tandvorming ten goede komt.
Het leerplan van Rudolf Steiner volgt de ontwikkeling van het fysieke verrassend gedetailleerd. De leerkracht moet bijvoorbeeld eerst de symmetrie van rechts en links in ogenschouw nemen en pas daarna de kinderen kennis laten maken met de symmetrie van boven en onder.
Deze twee opeenvolgende stappen kunnen ook worden waargenomen bij de vorming van tanden: In de regel begint het bij zesjarigen met de achterste kiezen, die nu pas groeien, vervolgens worden er vier tanden overgeslagen en de voorste, de snijtanden, worden op zevenjarige leeftijd gewisseld. Het is een beweging van buiten naar het midden, een verhouding van rechts en links. Pas in de tweede klas krijgt de relatie tussen boven- en onderkant, die er vanaf het begin is, een heel speciale betekenis. De achtjarige heeft in de boven- en onderkaak evenveel melktanden als blijvende tanden, wat betekent dat de verhouding boven-onder in evenwicht is. Nu is het begrijpelijk dat vormen waarin de rechts-links symmetrie, maar ook de boven-onder symmetrie (axiaal kruis) een rol spelen, voor de tweede klassers op het lijf geschreven.
Als we de kinderen in de tweede klas vertellen over de heiligen, komt het kruis weer ter sprake. Deze vorm wordt ervaren als een gebaar van houvast in de strijd tussen licht en donker. Beatus verslaat de draak door hem het kruis voor te houden.
Maar terug naar het tekenen van vormen. Hoe geeft elk individueel kind vorm aan het snijpunt in zijn symmetrische vorm? Veel kinderen hebben aanvankelijk geen vaste referentie naar het middelpunt. Het is zelfs wenselijk dat dit proces langzaam groeit en rijpt. Want pas als de kinderen in de derde klas het vermogen tot imitatie grotendeels hebben verloren, ervaren ze zichzelf, los van hun omgeving, als een middelpunt dat in zichzelf rust. Hier en daar echter, tegen het einde van de tweede klas, komt de nadruk op de middelpunten naar voren en dit zijn belangrijke voorbodes.
We kunnen nu de tandpatronen en symmetrievormen op de volgende manier analyseren (Arabische cijfers = blijvende tanden, Romeinse cijfers = melktanden):
Eerste klas
De zessen worden gevormd op zesjarige leeftijd, de enen worden gewisseld op zevenjarige leeftijd in de eerste klas. Het gebaar van buiten naar het midden is ook de basis van de symmetrievorm:

Tweede klasse
Volledige getalharmonie van boven en onder, rechts en links, hetzelfde aantal blijvende tanden als melktanden. Er ontwikkelt zich kruissymmetrie (aanvankelijk zonder vaste verwijzing naar het midden).
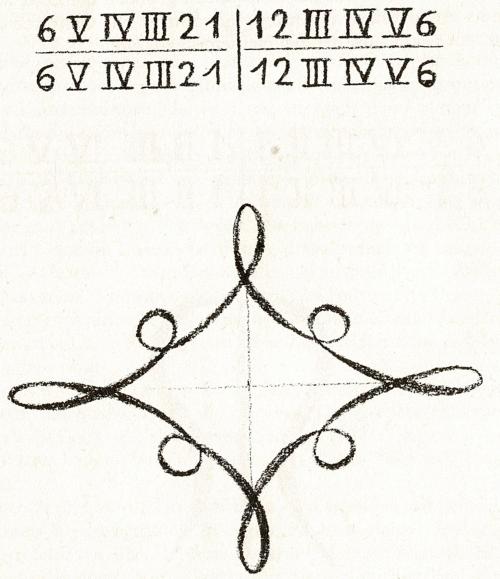
Derde klas
De zuivere symmetrie in tandvorming wordt doorbroken. Nu zijn vormen mogelijk die ten opzichte van het centrum op een volledig vrije manier gevormd worden, maar niet langer een starre symmetrie volgen. Voor deze ontwikkelingsfase beschrijft Rudolf Steiner vormen die “asymmetrische symmetrieën” bevatten, spanningen tussen binnen en buiten, centrum en periferie. (Zie zijn suggesties in de cursussen Ilkley 1923 en Torquay 1924.) Op deze leeftijd kan ook het gebonden schrift worden geïntroduceerd.
Dat wil niet zeggen dat je nu pas zou kunnen beginnen met gebonden schrift. Al in klas 1 zijn er veel vormtekeningen die tegelijk al iets van ‘verbinden’ in zich hebben; dat geldt nog meer voor de 2e klas. Wel lijkt mij dat in de 3e klas alle kinderen verzorgd schuin moeten kunnen (gaan) schrijven.

.
Vormtekenen: alle artikelen
Rudolf Steiner over vormtekenen: alle artikelen
Algemene menskunde: alle artikelen
Rudolf Steiner: alle artikelen op deze blog
Menskunde en pedagogie: alle artikelen
Vrijeschool in beeld: alle beelden.
.
3464-3261
.
.
.
