.
Rudolf Steiner: Echte pedagogie is menskunde. Die is al pedagogie en wordt didactiek als die vol leven in de praktijk wordt gebracht in het onderwijs en de opvoeding; dat wordt zelfs een pedagogisch-didactische levensovertuiging en daar komt het op aan.
Wegwijzer 359
Laatst ging ik een dag wandelen.
Uit de bus waarop ik wachtte, stapten enkele pubers.
‘Fijn naar school, jongens?’, riep ik ze toe.
“Schoool’ riepen ze in koor. ‘Saaaiiii’ en ze vervolgden luidruchtig hun weg.
Ik was wel benieuwd wat ze dan wel zo saai vonden en onwillekeurig kwamen mijn gedachten bij een paar sommen die ik de vorige avond op ‘Beter rekenen’ had gemaakt.
Algebraïsche vergelijkingen die me deden denken aan de wiskunde op mijn middelbare school.
We vroegen de leraar eens naar de zin ervan, maar hij kon het ons niet zo uitleggen dat we er op een of andere manier enthousiast voor konden worden.
Het bleef te abstract.
Het had geen relatie met onze belevingswereld.
Dat was in de jaren 1960, maar kennelijk ook al toen Steiner in 1919 de Waldorfschool begon.
En afgaande op de sommen in ‘Beter rekenen’ is dat nog steeds zo.
Ik weet niet of er methodes bestaan die dit probleem omzeilen.
Zo niet, dan kan ik de opmerking van de pubers wel plaatsen.
En als op de vrijescholen met methodes wordt gewerkt die geen rekening houden met de belevingswereld van deze leeftijd, dan is daar de algebra ook saai.
Al in 1928 stelde de wiskundige Ernst Bindel die door Steiner was gevraagd als leerkracht aan de Waldorfschool in Stuttgart, dit probleem aan de orde in het tijdschrift ‘Zur Pädagogik Rudolf Steiners’.
De gezichtspunten die hij naar voren brengt, zijn ook nu nog, na die bijna 100 jaar, actueel: hoe breng je de vergelijkingen zodat de leerlingen het echt interessant vinden.
Ik zie in dit artikel nauwelijks echt praktische voorbeelden, wel een bevlogen betoog van ‘de achtergronden’.
Dat kan ook vandaag een oproep zijn aan de wiskundigen om te onderzoeken waar ‘de stemming’ zit. Dat kan toch positief van invloed zijn op je voorbereiding op deze lesstof.
Dat de taal soms wat gedragen is, is voorstelbaar: het is een kleine 100 jaar geleden geschreven door een bevlogen leraar die (natuurlijk) direct door Steiner in zijn enthousiasme werd gesterkt.
.
Het probleem van de algebraïsche woordopgaven
.
Wanneer het leerplan van Rudolf Steiner stelt dat in de lesstof vergelijkingen behandeld moeten worden, samenhangend met het praktische leven; en hiermee wordt geen oppervlakkig pragmatisme bedoeld.
De oplossing van een vergelijking die ontstaat vanuit een omschrijving, doet een appel op de wil, of preciezer: het vraagstuk zou zo moeten zijn, dat het bij de menselijke wil uitkomt.
Helaas is in de tijd waarin we leven (1928!) een soort toeschouwersbewustzijn ontstaan en de opgaven zijn zo geworden dat ze de wil van de mens niet aanspreken.
{Het toeschouwersbewustzijn is alleen maar groter geworden: hoe vaak wordt een ongeluk gefilmd, zonder dat door de filmer hulp wordt geboden?]
En dus, hoe behandel je bij gebrek aan inzicht zo’n onderwerp nu.
Meestal worden er kant-en-klare vergelijkingen geoefend, die later ‘aangekleed’ worden. Het blijkt dat alleen leerlingen die al goed kunnen denken, wel meekomen. Waar ligt dat aan?
Een ingeklede vergelijking is een algebraïsch vraagstuk in de vorm van een tekst . P. Wijdenes zegt overeenkomstig (in Wiskunde voor accountants, dl. I, 1949): “Het is het voornaamste in de boeken eerst de theorie van de vergelijkingen te leren en daarna onderwerpen te geven, die met vergelijkingen kunnen worden opgelost.
De meeste van de nu gangbare opgaven zijn het resultaat van een ‘uitdokterend verstand’.
“Ingeklede vergelijkingen”. Net als louter een jurk, omhullen sommige fictieve processen uit het dagelijks leven de echte en maken de tekst van de opgave tot een schijntekst.
Maar bij elke omschrijving moet het grootste belang worden gehecht aan het feit dat het inhoudelijk klopt en niet gekunsteld is.
De verwijzing naar de verbinding met het praktische leven kan niet serieus genoeg worden genomen.
De huidige verzameling opgaven zit echter vol met opdrachten die vreemd zijn aan het leven.
Als je er beter naar kijkt, zie je iets bijzonders: Opvallend is dat de opdrachten doorgaans in de verleden tijd worden gesteld. “Een bouwaannemer kocht… Na hoeveel maanden vond de eerste betaling plaats?”
In deze stijl gaat het verder. Het is echt verrassend om zoiets te ontdekken. Er is a.h.w. een formele hang naar het verleden ontstaan. En dat is veel betekenend: want wanneer iets in het verleden wordt gezet, verstart het tot voorstelling.
De tijd die zo ingenomen is met de voorstelling, geeft er ook de voorkeur aan alles wat eens activiteit was, als een uitgeleefd, lijkachtig gegeven te nemen om het met het verstand te kunnen ontleden.
Sommige opgaven behoren zelfs tot het verleden van het verleden.
Een voorbeeld:
“Een koopman roosterde een mengsel van 16 kg koffie, 1 kg kostte
2,25 , met 14 kg van een tweede soort. Hoeveel kostte 1 kg van de tweede variëteit als 13 procent van het gewicht verloren ging tijdens het branden en de prijs voor 1 kg van het mengsel 30 cent meer bedroeg dan 1 kg van de tweede soort?”
Deze opdracht, in de verleden tijd gezet, was ooit ‘heden’ en het ging natuurlijk zo dat de koopman die de mix samenstelde naast de prijs van de eerste soort, ook de prijs van de andere soort moest weten – die hier gevraagd wordt! – vóór hij ging mengen – om dan een prijs vast te stellen waarvoor hij het mengsel zou moeten verkopen.
In plaats daarvan laten we de koopman mengen zonder van hem de prijs van de tweede soort te horen.
Op het eind zegt hij wel iets over de prijs van de gereedgekomen melange en wij moeten nu ‘terugbeschouwend’ de prijs van de tweede soort berekenen.
In het verleden zit eigenlijk nog een verleden. Zo’n opdracht is a.h.w. naast de eerste dood die nog te overwinnen is, een tweede dood gestorven: zo volkomen irreëel is deze dat die pedagogisch niet te verantwoorden is.
En zo zie je dat je het materiaal dat je zou moeten gebruiken, eerst moet onderwerpen aan een grondig onderzoek om er iets pedagogisch bruikbaars uit te halen.
Sommige opdrachten zijn alleen te gebruiken als je ze je verandert. Soms is een kleine verandering van de tekst, een andere nuancering, een andere tijd o.i.d. al genoeg.
De opgave hierboven is ook daarom een onding, omdat er twee gezichtspunten die ieder op zich wel kloppen, door elkaar lopen.
Bij opdrachten met onbekenden moet je een onderscheid maken tussen een vraag en een raadsel. Bij een vraag moet er steeds een serieuze wilsimpuls aanwezig zijn, een samenhang met het praktische leven.
Bij een raadsel wordt daarvan bewust afgezien: er moet iets te raden zijn. En je kan zeker wel positief staan tegenover vragen die als louter gedachtespelletje ontstaan zijn.
Een voorbeeld:
Het is wel geen opgave die tot een vergelijking leidt, maar anderszins zich toch
op rekengebied afspeelt:
Een Arabier laat bij zijn dood aan zijn drie zoons 17 kamelen na. In zijn testament staat dat de oudste zoon de helft krijgt, de middelste een derde en de jongste een negende. Maar met 17 paarden is dat niet te doen. Nu komt er een op de gedachte een kameel bij de buren te halen. En nu zijn er 18. De oudste krijgt de helft: 9; de middelste een derde: 6 en de jongste een negende: 2, dat zijn 17 kamelen, de 18e gaat weer – met grote dank – terug naar de buren. [1]
Iedereen kan aan de vraagstellingen zien dat het slechts een gedachtespelletje is; de vraag heeft geen masker voor om iets te lijken wat het helemaal niet is. En daarom is er geen gevaar. In tegendeel: deze raadsels impulseren op hun manier zeer sterk de wil om te denken zelf, ook al is het dan niet de wil die uit het denken voortkomt. Gedachtekrachten worden wel versterkt en het is interessant dat dergelijke opgaven uit het Arabisme stammen, waar het denken dat in deze tijd tot onwerkelijkheid leidt, daar als een echte kracht aanwezig was die van daaruit door persoonlijkheden als inspiratoren in onze cultuur van de nieuwere tijd werd gebracht.
(Volgens Rudolf Steiner behoorden ze in een vorige incarnatie bij die oudere cultuur. Wat deze nu in hun nieuwe aardse bestaan als erfenis en voortbouwend op het oude meebrengen, heeft niet meer die nieuwe oorspronkelijkheid die er in hun vorige leven nog was, en wat eerst zo aan de tijd was, kon nu ontaarden, zoals in de aangehaalde opdrachten in andere die we nu aantreffen.)
Maar om het gebied van de vergelijkingen te beginnen met dergelijke raadsels, lijkt ook niet zo’n goed idee.
Voor de leerkracht zou zo’n inleiding wel makkelijker zijn, maar het zou de leerlingen toch afleiden van de zakelijke ernst die nu eenmaal de basis is van alles wat met rekenen heeft te maken.
De vergelijkingen moeten geïntroduceerd worden in samenhang met het praktische leven. En dan is het vanzelfsprekend dat je eerst met de eenvoudigste begint. In wezen kunnen ze niet simpel genoeg zijn, want van de leerling vergt het de volle inzet van de nog jonge, ongeoefende denkkracht.
Als je op dit rotsige pad al wat obstakels hebt genomen, kan bij de leerkracht de vraag rijzen of hij nu zondermeer de leerlingen vergelijkingen voor kan schotelen om te oefenen. Mijn ervaring is dat ze graag aan de oplossingen werken.
Het is nu niet helemaal duidelijk wat Bindel dan met zijn leerlingen doet.
Enerzijds pleit hij voor ‘aansluiting bij het leven’, anderzijds krijg je de indruk dat hij tóch van te voren ‘droog’ oefent.
Dat laatste is op zich niet ongewoon, want in veel lagere klassen hebben de leerlingen al sommen gemaakt met een onbekende, b.v. bij het leren van tafels: Hoe vaak zit de 9 in de 63? is iets als 9 x ? = 63, het vraagteken is ‘de onbekende.
Dat horen de leerlingen natuurlijk allemaal te weten, dus kunnen ze, zoals Bindel dat beschrijft, vanuit hun meer ritmisch systeem dit soort onbekenden vinden.
Alleen bestaat dan het gevaar dat je de leerlingen door daar al te lang mee bezig te zijn, de smaak bederft voor de opdrachten die in woorden zijn gekleed. En ja, dit soort vergelijkingen (zonder woorden) ‘hangen volledig in de lucht.
Daarom het advies om er zo lang aan te werken dat de manier van oplossen wordt beheerst. Dan naar de ingeklede vergelijkingen.
Er is wel een erg aardige manier om de overgang te maken: dan moet je dat wat de vergelijking in symbolen zegt, simpelweg in een retorische vraagstelling zetten.
Dat is bij iedere vergelijking mogelijk.
Maar dan kom je niet met het praktische leven in aanraking, wel met iets wat leeft in de taal.
Het is goed om de opdracht in woorden niet al te beknopt te geven. Het moeten levendige zinnen zijn.
Een voorbeeld uit vele!
Het gaat om de som:
Welk getal is 3 groter dan de optelling van de helft ervan, een kwart en een zevende.?
Deze beknopte logische vorm past wel bij het verstand van de volwassene, maar niet bij dat van een kind. Dan zou je dit moeten zeggen:
‘Denk je eens in, dat je een getal opdeelt in breuken. Dan moeten de breukdelen samen weer niet zo groot zijn als het oorspronkelijke getal.
Maar wanneer je niet alle breukstukken hebt, heb je natuurlijk minder dan het begingetal.
Nu moet je een getal nemen en dat zo verdelen dat je eerst de helft neemt, dan een vierde en ten slotte een zevende deel. Deze drie breukstukken zijn samen natuurlijk minder dan het getal dat je nam; er blijft nog wat over. Bij welk getal zou er 3 overblijven?
Dit is dus een geval waarbij het taal-retorische de wiskundige symbolen omschrijft.
Dit is een van de voorbeelden die historisch overgeleverd zijn, zoals deze:
Edele Pythagoras, gij telg van de Muzen van Helicon,
zeg aan mij die het vraagt: hoeveel jongeren strijden in de arena van de wetenschap in dit huis om de wedsstrijdprijs?
Ik zal het je zeggen, Polykrates: de helft bedrijft de voortreffelijke mathematica: een vierde daarentegen is bezig met de natuur, de onsterfelijke; een zevende echter hult zich in stilzwijgen, zij bewaren de kennis in hun hart. Tel daar dan nog drie vrouwen bij, onder wie Theano: zoveel priesters bracht ik bij de Pierische muzen.
In het oeroude Egyptische wiskundehandboek van Ahmes komt de volgende opgave voor: ‘Kijk, daar komt de koeienherder met 70 ossen. De rekenaar vraagt aan de herder: hoeveel breng je van je talloze vee mee? De herder antwoordt: ik nam twee derde van een derde van mijn gehoornde vee mee: dus reken mijn hele bezit maar uit.
Er zijn nog veel meer van deze voorbeelden die laten zien dat ook vroeger al de verbinding van rekenen met taal geliefd was.
In die tijd wordt ook de oplossing sprekend gegeven.
De ontwikkeling naar nu moet er echter niet in bestaan dat we van het element taal afzien, maar wel dat de taal uiteindelijk ondergeschikt is aan de verstarrende krachten. De tegenstelling leven – dood mag wel ervaren worden, niet de dood alleen.
De leerling moet zich bewust worden van wat er gebeurt als je van tekst naar de vergelijking gaat.
De tijd waarin we leven vraagt een sterker Ik-bewustzijn.
Het Ik is doorgedrongen tot in het fysieke lichaam en heeft daarmee het astraal- en etherlijf achter zich gelaten. Daarom neemt het voelend waar wanneer het levende wordt gedood. Zoals de Ik-organisatie bij het verteren van het fysieke voedsel in de darmen de vreemde vitaliteit verdrijft om deze door de eigen vitaliteit te vervangen, zo voelt datzelfde Ik bij de vertering van geestelijk voedsel eveneens het doden van de aanwezige vitaliteit.
Het is goed om tegen het eind van het onderwijs steeds meer die opgaven te nemen die belangrijk zijn, zonder dat je dat misschien op het eerste gezicht ziet.
Je hebt b.v. de som: op een rondlopende weg moeten twee leerlingen vanaf dezelfde plaats tegelijkertijd in tegenovergestelde richting lopen, de ene zo snel dat deze in 2 minuten rond is, de andere zo langzaam dat hij er 5 minuten over doet. Elke ??? minuten passeren ze elkaar.
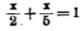
De vergelijking ziet er zo uit:
wanneer je onder x het aantal minuten tot aan iedere ontmoeting verstaat.
Deze x kan zo genoteerd worden:
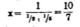
(onder de breukstreep staat: 1/2 + 1/5
Elke 1 3/7 minuut komen ze elkaar tegen en het interessante is dat vóór de langzamere een keer rond is, de snelle loper hem 3x gepasseerd is.
Zo’n schijnbaar onbelangrijke opgave heeft een grote achtergrond. Alleen daarom al is deze van betekenis omdat het resultaat de precieze helft is van het harmonische midden tussen 2 en 5;
het harmonische midden tussen 2 getallen a en b wordt uitgedrukt door:

Zou je op een monochordsnaar naast de grondtoon nog de reine kwint en het octaaf van de terts die daar tussen ligt aanstrijken, dan zijn de 3 snaarlengtes
volgens dezelfde wetmatigheid met elkaar verbonden als de drie tijden hierboven.
De harmonie van de drie genoemde tonen heeft een prachtig oplossend afsluitend karakter.
In onze opgave hebben we ook te maken met een wonderbaarlijk harmonische realiteit. Er ligt namelijk een verheven kosmische wetmatigheid aan ten grondslag: in ongeveer 26.000 jaar verplaatst het lentepunt zich door de dierenriem en in de viervoudige tijd, in meer dan 100.000 jaar beweegt de plaats zich waar aarde en zon in de loop van een jaar het dichtst bij elkaar staan, het zgn. perigeum of perihelium, in tegenovergestelde richting zoals het lentepunt in de dierenriem; beide komen elkaar dus rond alle 20.800 jaar tegen.
Zo’n opgave als hierboven verbindt niet alleen met het praktische leven, maar ook met het kosmische.
Wat zullen de leerlingen opkijken wanneer je al die wetmatigheden aan de hand van de som in het begin, in het onderwijs mee kan nemen!
Je kan de som zo veranderen dat de lopers ook in dezelfde richting lopen; dan kreeg je een beeld van hoe de maan met de zon loopt; je wekt begrip voor de relatie tussen een sterrenjaar, sterrenmaand (siderisch) en een synodische maand.
En je gaat altijd als je bij de keus van opdrachten je richt op inherente wetmatige bewegingen.
Dan wordt de wil op een gestructureerde manier gestimuleerd. Tegelijkertijd krijg je door zulke opdrachten het element tijd bij de berekening en tijd maakt een wezenlijk deel uit van al het reken-wiskundige.
Laten we dus duidelijk zijn dat de woordopdrachten die voor de jeugd adequaat moeten zijn, zich op de een of andere manier op hun wil moeten werken. De wil is in tegenstelling tot de voorstelling een zielskracht die op de toekomst is gericht. Het hoort nog niet bij de jonge mens om terug te kijken naar het verleden; alleen oude mensen doen dat graag. De jongere wil vooruit, wil ouder zijn dan hij werkelijk is. Het is daarom het beste als de op te lossen vraagstukken voor de toekomst gesteld worden of in de uitdrukking van ‘zou graag willen, dat zou fijn zijn enz. gekleed worden. Dan worden ze met sympathie ontvangen. Ook moet je erop letten, zoals al werd gezegd, dat in de som zoveel mogelijk de begrippen levend in de taal aanwezig zijn, zodat niet alleen een droge lijst met de benodigde gegevens opgesomd wordt. Als wezen van vlees en bloed moeten ze de leerlingen tegemoet treden, zodat deze veel activiteit kunnen ontplooien om het skelet eruit te pellen door over te gaan naar de bepalende vergelijking; hij kan zich dan veel sterker bewust worden van zijn eigen vormende krachten dan wanneer de opdracht zelf al een skelet is.
Als de sommen goed zijn gekozen, brengen ze ofwel de hele persoon met alle drie zijn zielsvermogens ofwel de gevoelsmens, in beweging. Dan doen ze geestelijk iets belangrijks.
Want de leeftijd die de leerlingen met hun 12e jaar binnengegaan zijn, wordt gekenmerkt door het feit dat de mens nu vanuit een natuurlijke eenheid uiteen dreigt te vallen in een polariteit: die van hoofdmens en die van instinctmens; als daar niet het verbindende midden gevonden wordt, wordt deze breuk die door de ziel loopt, voor de rest van het leven bestendigd. Het is het kenmerk van onze beschaving dat deze mensen daartoe brengt en niets biedt om het evenwicht te herstellen.
Moet je naast de zorgvuldig gekozen opdrachten de leerlingen ook meegeven wat volgens ons de spirituele betekenis is van de bepalende vergelijkingen? Moeten we vertellen over de skeletfiguur en het verband tussen algebra en de krachten van de dood? Dat zou een vergissing zijn, want dan zouden we de vrijheidssfeer van de jonge mens geweld aandoen. Hij zou nog niet in staat zijn zich daar kritisch tegen te verdedigen. Natuurlijk kan je de leerling erop wijzen dat er iets skeletachtigs in de hele structuur van een vergelijkingsoplossing zit, wanneer je
volgens de aanwijzingen van Rudolf Steiner wat een formule moet worden, in een beeld geeft. Je geeft hem dan niets meer dan bouwstenen waar een betekenisvol gebouw van kan worden neergezet. Het bouwen zelf mag pas plaatsvinden als in de mens de kracht kritiek te hebben en te twijfelen, sterk genoeg geworden zijn. Je kan erover denken, om bijvoorbeeld als de algebra in klas 11 ophoudt, enkele aanwijzingen te geven over de diepe laag van dit gebied, en dan, wanneer de leerling vijf volle jaren van voortdurend groeien, met deze dingen bezig is geweest, zou je bij hem de nodige bereidheid kunnen vinden.
Vooropgesteld moet worden dat de leraar gedurende deze vijf jaar zelf voor zijn leerlingen gevoelsmatig leefde met deze samenhangen en met pedagogische wijsheid alle individuele maatregelen daarbij afgewogen heeft. Hij moet b.v. in zichzelf beleven hoe de vergelijking horizontaal een beweging maakt, hij moet die wisselwerking tijdens de ontbinding tussen formule en identiteit innerlijk ervaren, bewust en ook extern zichtbaar maken en pas nadat dit voldoende duidelijk door de leerlingen opgenomen is, de schrijfwijze wezenlijk korter maken en de gang van de berekening met het vereenvoudigende algoritme introduceren. Dit betreft het overbrengen van de termen van de ene naar de andere kant. Het moet voor hem steeds een punt van zorg geweest zijn om de individuele vergelijkingen als het enigszins mogelijk is zo onder elkaar zo te schrijven dat de gelijktekens onder elkaar staan en elke vergelijking niet meer dan één regel in beslag neemt. De verstandige leraar wijst zulke ogenschijnlijke bijkomstigheden niet als een onbenulligheidje af, de wervels van de ruggengraat liggen ook niet als iets triviaals precies onder elkaar.
Alleen al het loutere gevoel van schoonheid, waarop je bij de leerling een beroep kan doen, verbiedt elke andere manier van opschrijven.
Wat voortkomt uit de innerlijke werkelijkheid is ook mooi; alleen is het hier niet langer de schoonheid van het schilderachtige, maar al die van het muzikale, wat niet beschouwend, maar beleven wil worden ervaren als iets van de actieve wil.
Wat hier over de vergelijkingen is gezegd, geldt gedeeltelijk ook voor de behandeling van formules. Ook dan is het b.v. nodig dat formules niet uit het niets worden bedacht, maar dat er formules worden gekozen die ook in de cultuurgeschiedenis van betekenis zijn geweest. Een belangrijke plaats nemen de
binomiale in met de vele andere die daaruit ontwikkeld kunnen worden.
Het zal ook zeer nuttig zijn voor de leerling als je hem de eigenschappen van de haakjes uitlegt en in bredere zin, dat tot een beleving maakt die enthousiasmeert.
Je kan je altijd zo uitdrukken dat je je aanpast aan wat de leerling kan begrijpen. Je kunt tegen hem iets zeggen als:
‘We hebben de mens met de door God gegeven kenniskracht en hij heeft overal de opdracht vanuit zijn inzicht de materie die de aarde hem geef, met ijver om te vormen.
De geest van de mens moet zijn kracht uitproberen op aardse stoffelijkheid en voor je latere leven oefen je dat al op school in de wiskunde, wanneer je wiskundestof omvormt.
Om ook te zien wat we hebben gedaan, plaatsen we de gevormde wiskundige stof onder de ongevormde en verbinden deze door een lijn die van boven naar beneden loopt; het is alsof we onszelf vormend vanuit de hemel naar de aarde, van boven naar beneden bewegen. En om ook te zien dat het materiaal nu is gevormd, willen we denken aan de kunstenaar die met het beeld dat hij in zijn hoofd had zijn handen aanspoort zodat deze de maakbare aardematerie naar het beeld van de geest vormgeeft.
Daarom omsluiten wij het gevormde cijfermateriaal als met twee handen
en noem ze haakjes. Alleen met je handen, kun je iets goed omvatten.’
Bij dergelijk onderwijs kan je ervaren dat deze symbolen en beelden uit de diepste mens komen en als vanzelf door de jonge mens worden opgenomen en met de diepste belangstelling zal hij nu de door de leraar gestelde taken doen.
[1] Er bestaat nog een variant.
.
Ernst Bindel
Voor zover ik weet is geen van zijn boeken in het Nederlands vertaald.
Algebra: alle artikelen, waaronder ook de behandeling van vergelijkingen
Klas 7: alle artikelen
Klas 8: alle artikelen
Menskunde en pedagogie: alle artikelen
Vrijeschool in beeld: alle beelden
.
3278-3085
.
.
.
.
.
