.
Als we eens iets uit een meetkundeperiode op bv. een Facebookpagina of op Pinterest zien, zijn het meestal de prachtig(st)e tekeningen.
Voor de buitenstaander lijkt het er dan op, dat meetkunde slechts het tekenen van bijzondere figuren is.
Wie bv. op deze blog de opbouw van een meetkundeperiode in klas 6 volgt, ziet echter dat het om heel andere dingen gaat dan deze prachtige tekeningen.
Het gaat echt om meetkunde, bv. de hoeken, de figuren als driehoek, vierkant enz. De graden, allerlei eigenschappen, symbolen.
Wanneer je die beheerst, kan je bv. in een cirkel een 8-hoek maken en ja, ten slotte kun je de ontstane vormen kleuren – als een kunstzinnige afronding.
Je moet echter ook met de meetkunde kunnen berekenen.
In onderstaande opgaven gaat het om gradenberekening van hoeken.
Belangrijk is een bepaalde systematiek, bv.
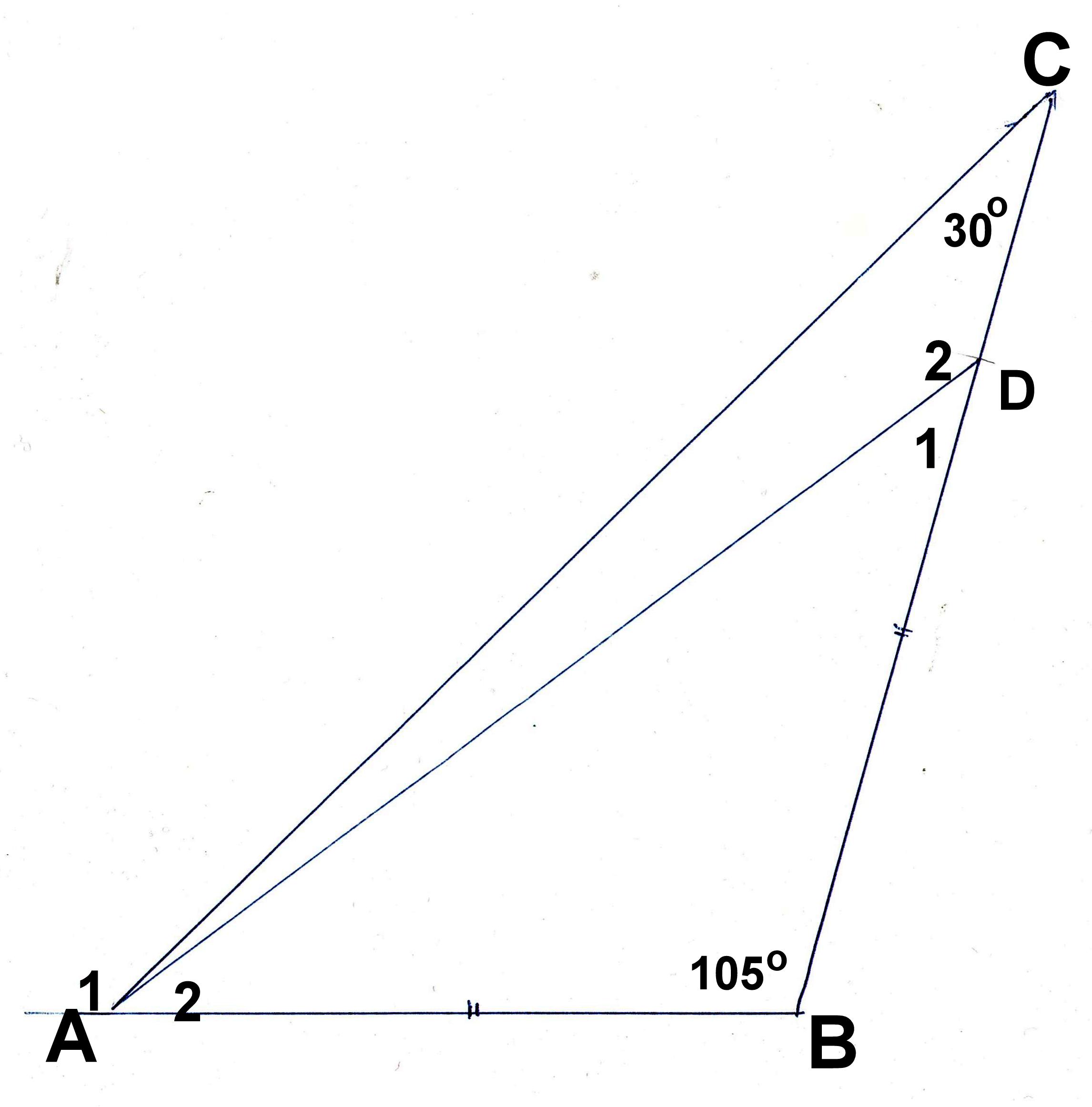
Gegeven: Δ ABC
AB = AD
∠C =30°
∠B =105°
Gevraagd: hoe groot is ∠A1
Antwoord:
Kan gegeven worden als de leerlingen hebben geleerd dat de 3∠ van een Δ samen 180º zijn; dat de basishoeken van een gelijkbenige Δ gelijk zijn.
En dat de basis niet altijd de horizontale lijn is.
Ook het schrijven met de symbolen hoort erbij.
Te bewijzen:
De grootte van ∠A1
Bewijs:
Δ ABD is gelijkbenig. De tophoek is 105°; voor de andere 2 blijven 75° over:
∠A2 = ∠D2 = 75° : 2 = 37,5°
∠C = 30° ∠B = 105°, samen 135° ; over voor ∠A1/2 45°, waarvan ∠A2 37,5°
→ ∠A1 = 7,5°
Wanneer de leerlingen de nevenhoekeigenschap kennen: de 2 nevenhoeken zijn samen 180°, dan is ∠D1 142,5°, samen met ∠B = 30° = 172,5°; voor ∠A1 blijft 7,5°over.
0-0-0
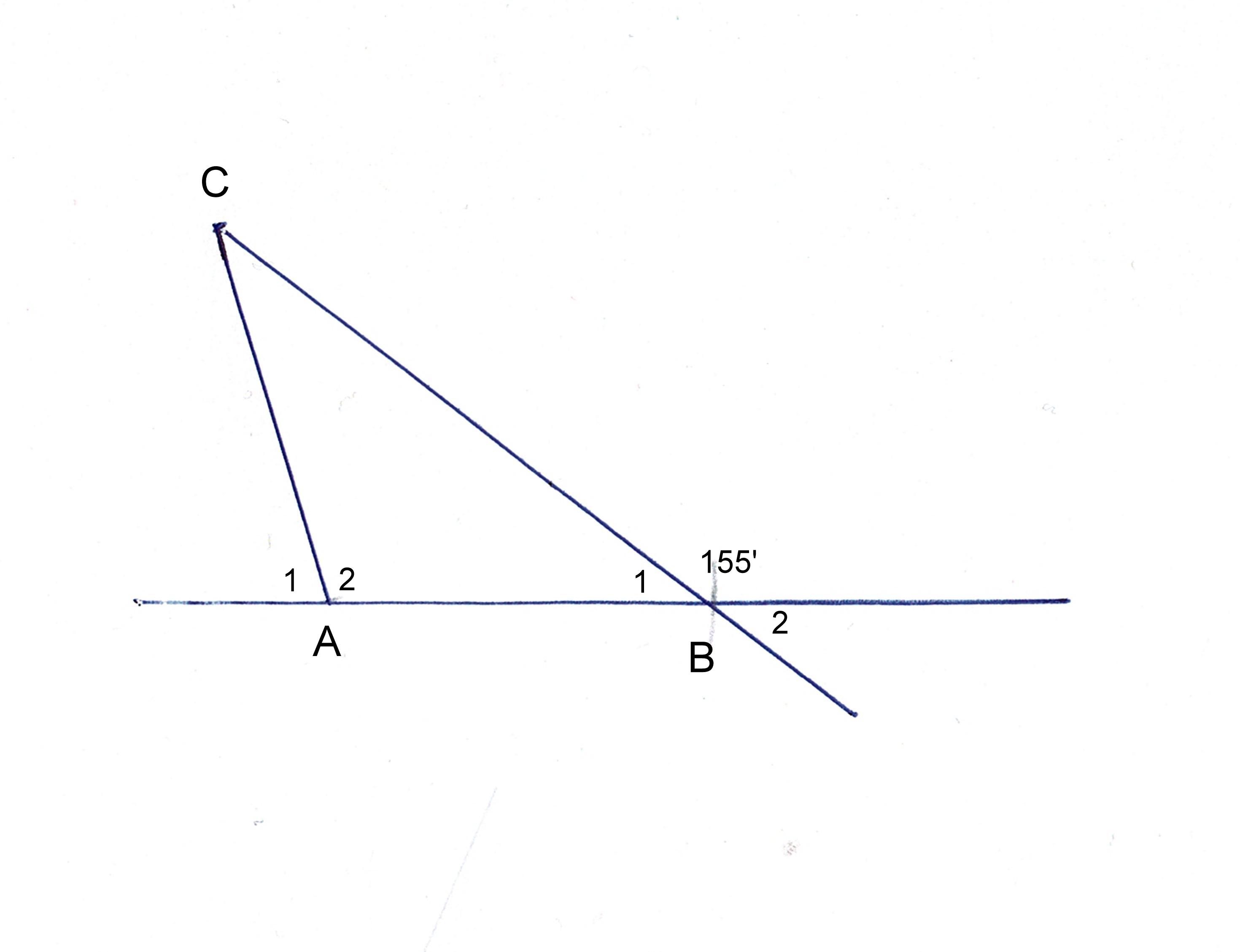Gegeven: Δ ABC
AC = AB
∠B = 155º
Te bewijzen:
Hoe groot is ∠A1
Bewijs:
∠B1 = 180º – 155º = 25º
Δ ABC = gelijkbenig ∠B1 = ∠C = 25º
∠A2 = 180º – (25º + 25º) = 130º
∠A1 = 180º – 130º = 50º
0-0-0
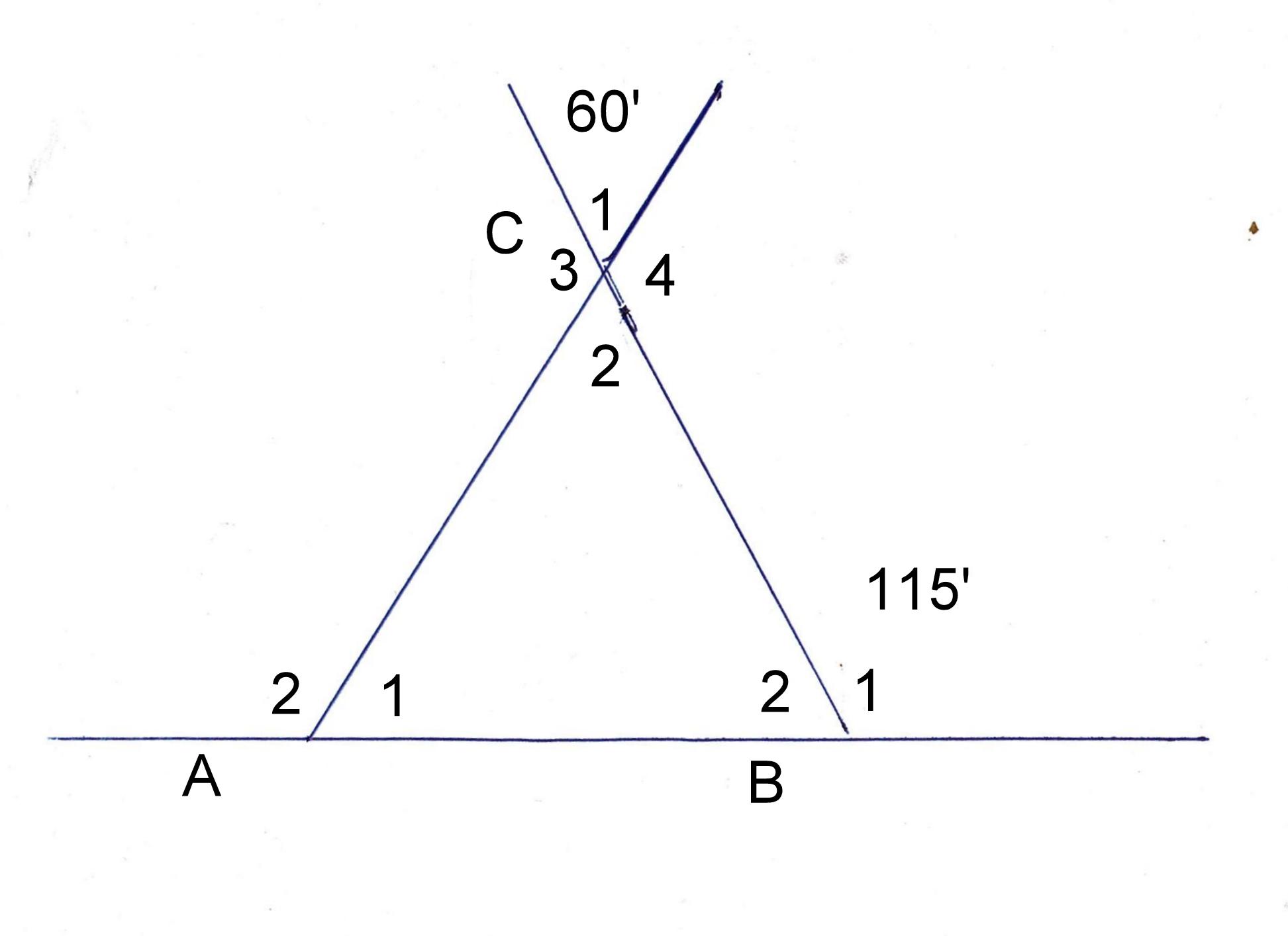Gegeven:
Δ ABC
∠B1 = 115º
∠C1 = 60º
Bewijs:
De grootte van alle andere ∠∠
Bewijs:
∠B2 = 180º – 115º = 65º (nevenhoeken samen 180º)
∠C2 = 60º (overstaande ∠∠ gelijk)
∠A1 = 180 º- (65º + 60º) = 55º
∠A2 = 125º (nevenhoek)
∠C3 = 120º (nevenhoek)
∠C4 = 120º(overstaande ∠) (tevens nevenhoek)
0-0-0
Gegeven
lijnstuk a // lijnstuk b
∠A = 130º
Te bewijzen:
Grootte ∠B1
Bewijs:
Verleng b tot c
Er ontstaat een Δ ABC
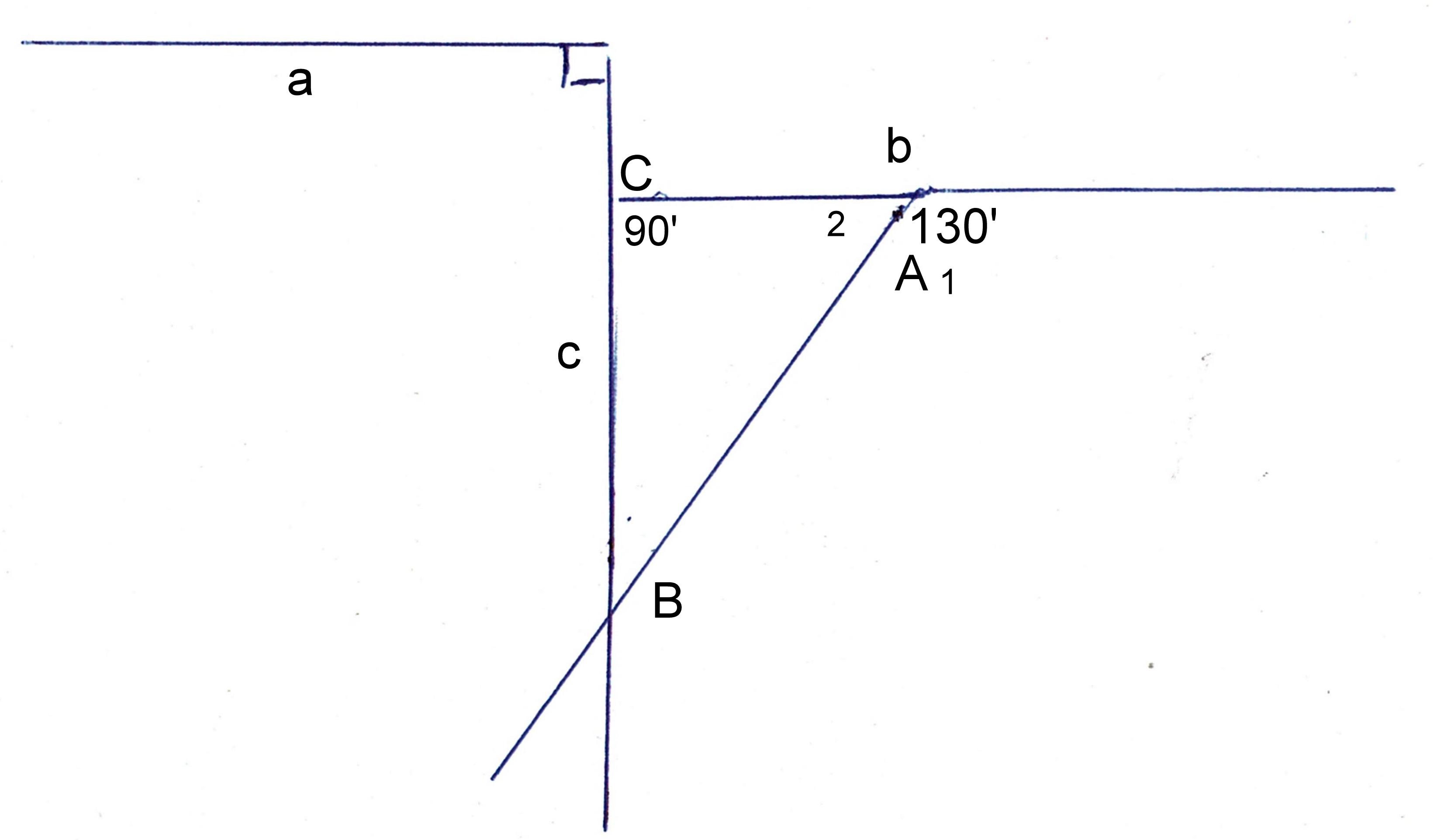
waarvan ∠A2 = 50º (nevenhoek)
∠C= 90º
∠B1 = 180º – (90º + 50º) = 40º
0-0-0
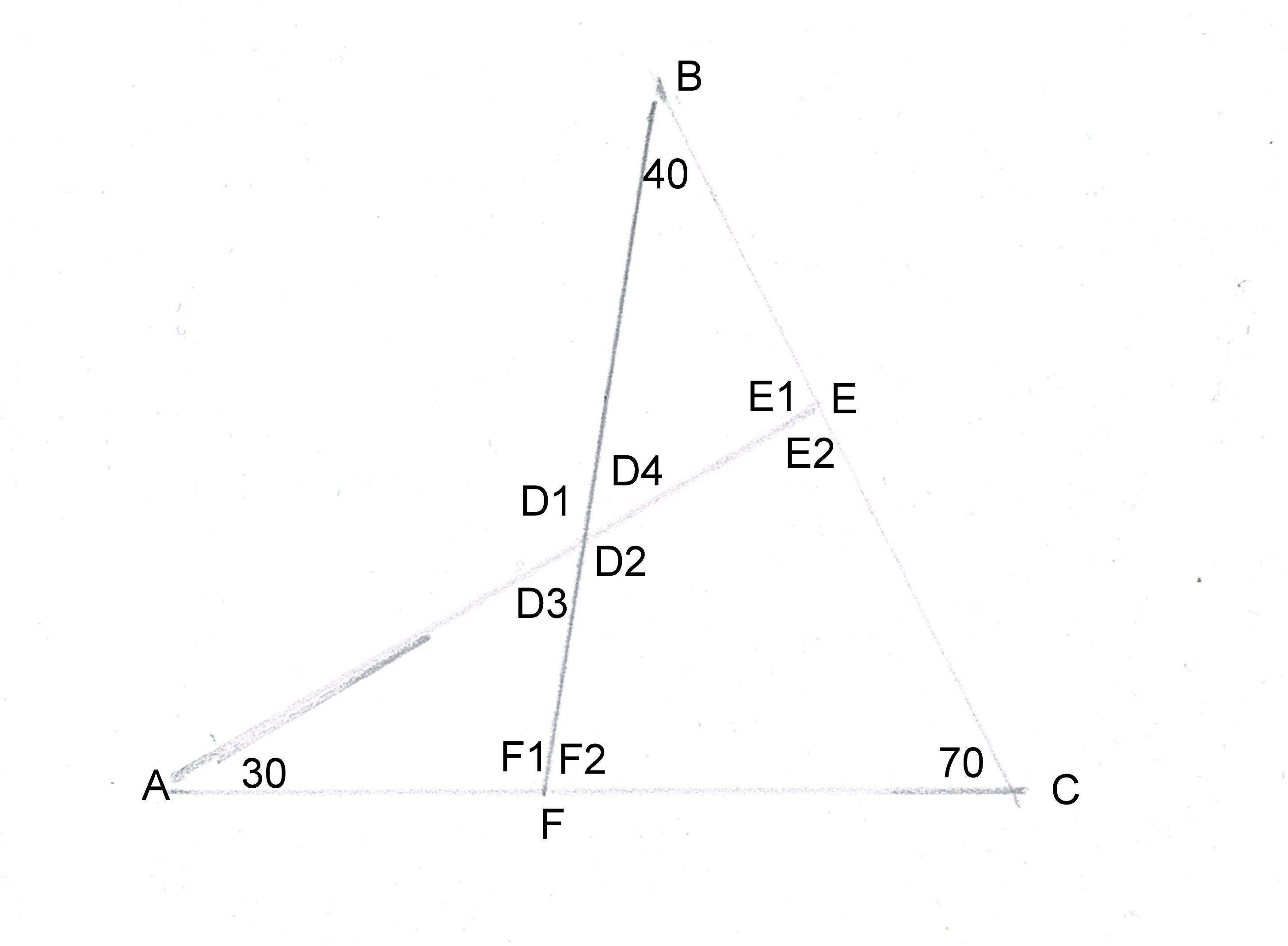
Gegeven
(O.A.) Δ AE2C , Δ BCF2
Te bewijzen:
Hoe groot is ∠ D2
Bewijs:
In Δ BFC =∠ F2 70º (180 – 40 – 70)
∠ F1 is dan 110º (180 – 70)
∠ D3 is dan 40º (180 -110-30 = 40)
∠ D2 is dan 140º (180 – 40)
Je zou deze opgave kunnen uitbreiden met:
Bereken alle hoeken.
Wat weet je van Δ BD4E1
Gelijkbenig: ∠ D4 = 40º
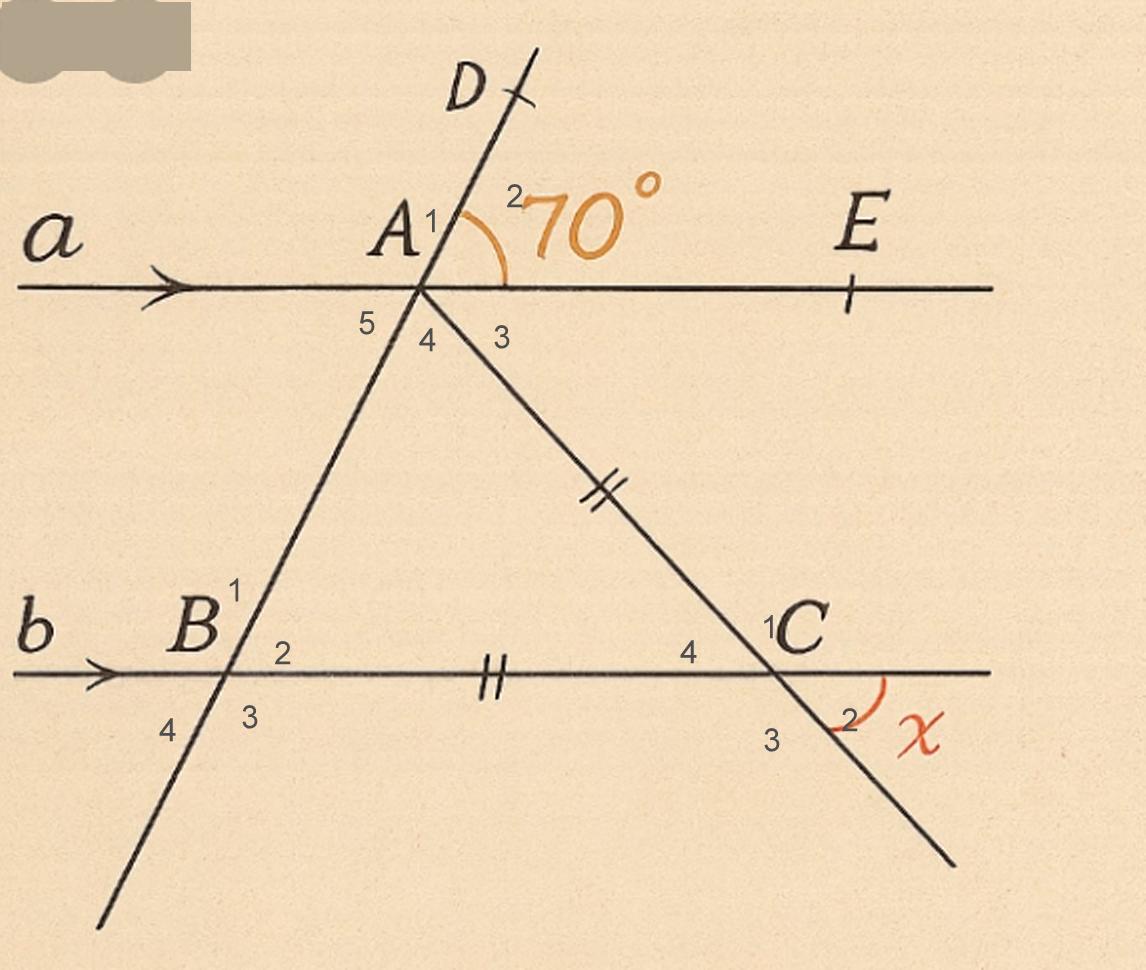
Gegeven:
Lijnstuk a // b
∠ A1 = 70º
AC = BC
Te bewijzen:
Grootte van ∠ C2
Bewijs:
∠ A1 = 110º (nevenh.)
∠ B1 dus ook
∠ B2 = 70º
Δ ABC = gelijkbenig
∠ A4 =∠ B2 (gelijke basishoeken)
∠ C4 = 40º 180º-(70º+70º)
∠ C4= ∠ C2 (overst. h)
∠ C2 = 40º
MET CIRKELS
Als je de oppervlakte hebt behandeld van bv. de rechthoek, het vierkant en de driehoek, en de stelling van Pythagoras, zijn daarmee ook opdrachten uit te voeren.
Steiner noemde verschillende keren ‘de abstractie van een rekensom’ als vaak een opgave ‘die buiten het leven staat’ – zijn verschillende keren gebruikte som om de gemiddelde leeftijd uit te rekenen van grootvader, vader en kleinzoon. Die leeftijd bestaat simpelweg niet.
Ook bij wiskunde sommen zou het mooi zijn als je opgaven kan geven die ‘in het leven’ voor kunnen komen.
Zo bv.:
Je hebt een vierkante plaat hout nodig van 75 x 75cm. In de schuur staat nog een ronde plaat hout met een diameter van 100 cm. Kan die vierkante plaat daaruit.
Je maakt een tekening:
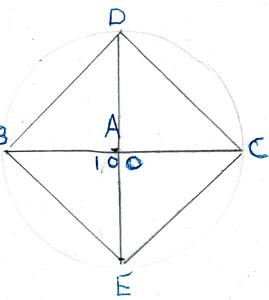
BC = 100 cm
De straal (r) is 50cm.
Richt in A de loodlijn op. DE.
Verbind BDCE = vierkant.
DC = hypotenusa van DAC
Met Pythagoras de som van de kwadraten van DA en AC.
Die zijn 50: 2500 + 2500 = 5000.
Je moet 75 x 75 hebben, dat is 5625.
Te weinig: de plaat van 75 x 75 kan er niet uit.
(Eigenlijk hoef je deze tekening niet zo volledig te maken. Het zien van ADC is al genoeg. En als je gaat inzien dat je zo’n vraagstuk ook meteen rekenkundig kan oplossen, heb je geen tekening nodig: Het kwadraat van 75 is kleiner dan 2x het kwadraat van 50).
wordt voortgezet
.
Meetkunde klas 6: alle artikelen
VRIJESCHOOL in beeld: 6e klas: alle beelden
.
3406-3204
.
.
.
.
VRIJESCHOOL 